About me:
I conducted my PhD thesis at the University of Helsinki, under the direction of Prof. Kari Astala, on quasi-conformal functions, calculus of variations and their application to material science. Motivated by this last aspect I joined S. Müller's group at the Max-Planck Institute for Applied Mathematics in Leipzig. After my postdoctoral stay I obtained a Ramón y Cajal scholarship and joined the Universidad Autónoma de Madrid (UAM), where I am full professor of applied mathematics since 2020.
In 2012 I was granted with an ERC CONSOLIDATOR "Geometric function theory, Inverse Problems and fluid dynamics", ended in 2018. Currently I lead the UAM Node of Quamap (ERC Advanced Grant), the UAM Node of Agapi 2018-2021 and the group of inverse problems and mechanics of the UAM. I have also been involved in the three "Severo Ochoa" accreditations awarded to the Institute of Mathematical Sciences (ICMAT), being a guarantor and currently a member of its executive committee.
Although my scientific interest has changed over time, it has always lied at the intersection between mathematical analysis and applied mathematics. Applied problems with a strong theoretical component or theoretical problems with a potential use in applications. Quasi-conformal mappings are particularly dear to me, which on the one hand investigate how many of the beautiful ideas of complex analysis can be extended to less rigid functions and, on the other hand, constitute a sufficiently regular class of elastic deformations to be handled with mathematical technical analysis.
Although quasi-conformal mappings emerge in practically every aspect of my research, there are three topics that interest me fundamentally: calculation of vector variations and non-linear elasticity, the inverse problems and the study of turbulence in fluid mechanics.
I have directed three PhD thesis and more than 10 long term postdoctoral researchers. In the teaching section, topics of interest for final degree and master's work are described. Those interested please contact: daniel.faraco at uam.es. Job application calls are regularly opened at the UAM.
Some images of my scientific activity

Solar flares
The equations of hydrodynamic magnet (MHD) govern solar plasma and nuclear fusion. In a joint work with Lindberg and Székelyhidi Jr., we have proved that there are theoretical solutions of MHD that preserve magnetic helicity and dissipate energy, as observed in the experiments. With Lindberg we have proven that the preservation of magnetic helicity at the ideal limit is responsible for solar flares. These generate the solar wind that interacts with the Earth's magnetic field to generate the bright aurora borealis.

A diffracted plane wave
Inverse problems want to find out the question, knowing the answer.
In quantum mechanics, one wants to infer information about electromagnetic potentials by knowing the diffracted wave. Together with Astala and Rogers, we have developed a programme that relates this inverse problem to the convergence to the initial data of the Schrödinger equation.

Turbulent fluid mixtures
Fluids develop instabilities due to discontinuities in the interface due to differences in density (Rayleigh-Taylor)
or speed (Kelvin-Helmholtz). These instabilities make it impossible to describe them with traditional tools based on partial derivative equations. Together with Cordoba and Castro, we have combined the convex integration technique with semi-classical analysis to generate a new framework for modelling these situations.
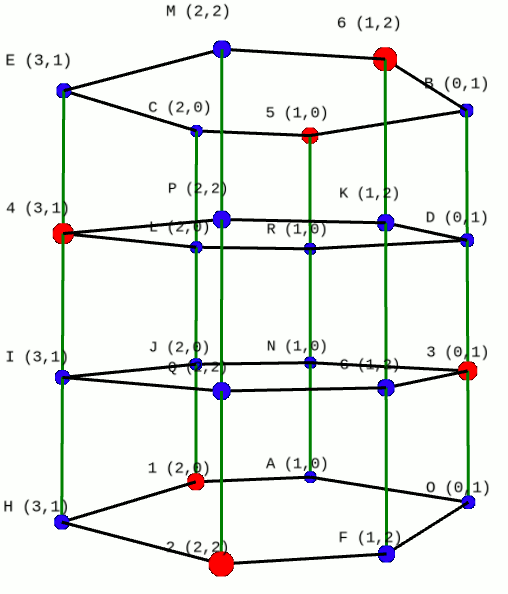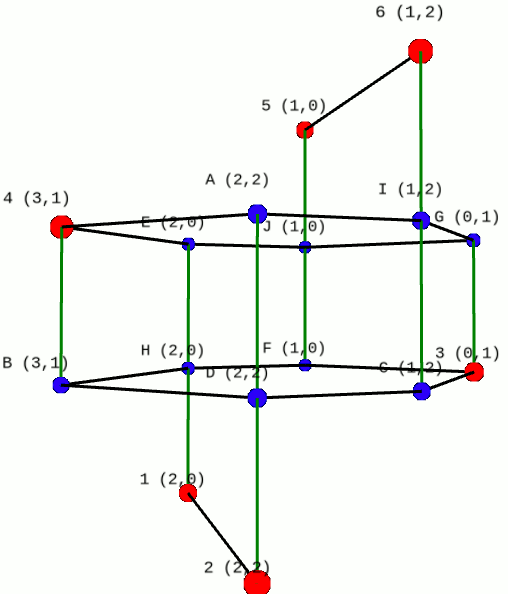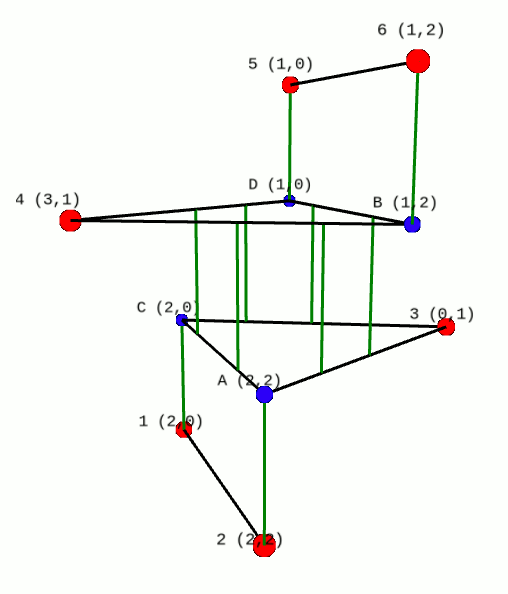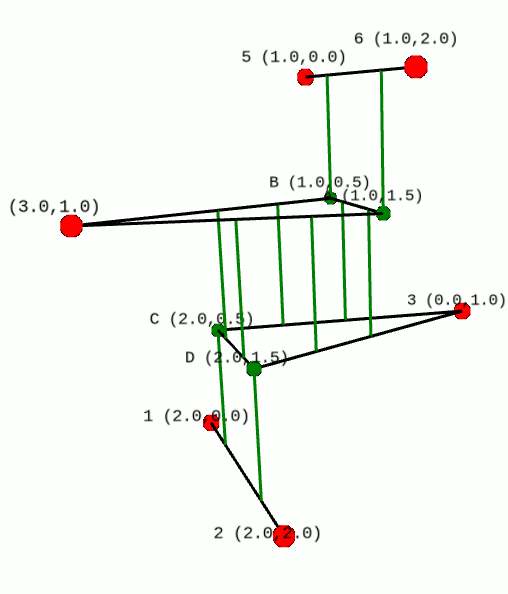
D-Convex envelopes in Variation Calculation
In the calculation of vector variations, the classical notion of convexity is replaced by weaker notions such as quasi-convexity, or convexity along range one directions. There are plenty of theoretical results but these notions of restricted convexity are very difficult to manipulate. The figure illustrates a recently developed algorithm to calculate the (2+1) convex envelope together with Angulo and Gutierrez (courtesy of P. Angulo).
Degraded fluid mixtures
The Mengual thesis deepens the fluid mixture in the unstable case. In the video on the left, the heavier dark particles are mixed with the lighter ones on a macroscopic level. On the right, we can see the average sharing (macroscopic). The right one corresponds to the solution by convex integration, related to the sub-solution on the right. The videos correspond to a simplified stochastic model (courtesy of F. Mengual).

Five points with a large rank-one convex hull
Five points with a large rank-one convex hull. We have discovered that these structures are the building blocks for a compensated compactness theory regarding electromagnetism.

The famous Douady Rabits
Our recent progress in relation with Morrey conjecture consists in deforming in an holomorphic manner the boundary values to a generic test fucntions. Such holomorphic deformations are inspired in holomorphic deformations of fractals such as the famous Douady Rabits.

At Einstein office, at IAS 2022, taking part of a special year in convex integration.







