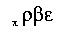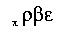Overview
In general terms, our project considers various questions of harmonic analysis and their interactions with areas of number theory, combinatorics, ergodic theory, and mathematical physics. All these lines are unified by methods related, in one way or another, to Fourier analysis. More precisely, we consider two big blocks:
-
Number theory and analytic applications.
The main topic here is analytic number theory although we also intend to explore the interplay between arithmetic and other areas, for instance, spectral theory, PDEs and mathematical physics. Some of the problems are not so close to number theory, which can act as a motivation, and, indeed, we also plan to approach a purely analytic problem coming from geometry.
-
Arithmetic combinatorics and higher-order Fourier analysis.
This block unfolds in the following three main directions: firstly, progress in the theory of higher-order Fourier analysis; secondly, the development of practical applications of higher-order Fourier analysis, especially through algorithmic implementations; finally, work on several problems in arithmetic combinatorics about certain approximately algebraic structures in abelian groups.
Goals for the period 2025-2028
These are the concrete goals we propose ourselves for the current period of our grant:
-
Improve the best-known result about the lattice point problem for the sphere and study some other lattice point problems.
-
Use the spectral theory of automorphic forms to get arithmetic results for the number of representations by quadratic binary forms.
-
Explore the use of arithmetic methods in the theory of exponential sums to get results in theoretical physics and PDEs (for instance, the existence of solutions with plateaux or fractal behavior under rough initial conditions).
-
Consider minimal surfaces in a generalized sense and study their regularity.
-
Explore the applications of the new spectral algorithms in higher-order Fourier analysis introduced by Candela, González-Sánchez, and Szegedy.
-
Use the new ideas provided by the spectral approach to higher-order Fourier analysis, as well as the recent works of Candela, González-Sánchez, and Szegedy on the theory of this area, to obtain a new proof of the inverse theorem on certain finite abelian groups with improved bounds, especially the finite cyclic groups.
-
Make progress towards the Jamneshan-Tao conjecture in higher-order Fourier analysis.
-
Explore new applications of the recently proved Marton (or Polynomial Freiman Ruzsa) conjecture in arithmetic combinatorics.
-
Make further progress towards a full resolution of the 3k-4 conjecture modulo a prime.
-
Make further progress on Motzkin's problem in compact abelian groups.