The matrix of the DWT


With the normalization as in my signal processing course, the Discrete Wavelet Transform (DWT) is a unitary linear operator on the N dimensional space. Hence it has an N dimensional unitary matrix.

We consider here the cases Haar (D2), D4 and D12, coming from the filters [0.70711, -0.70711], [-0.12941, -0.22414, 0.83652, -0.48296] and [-1.0773e-03, -4.7773e-03, 5.5384e-04, 3.1582e-02, 2.7523e-02 -9.7502e-02, -1.2977e-01, 2.2626e-01, 3.1525e-01, -7.5113e-01, 4.9462e-01 -1.1154e-01].

Given a filter f, the function wav_tr computes the DWT of a signal vector or of a collection of them. In particular, wav_tr( fd4, eye(N)) gives the matrix of the DWT.

DISCLAIMER: It is clear revising the code that this is not an efficient way of computing this matrix because it disregards the internal structure indicated below. The code has only academic purposes. I intended to write something quick, versatile and easy to understand.

With the octave code below we get that using the Haar filter the matrix for N=4 is

0.50000 0.50000 0.50000 0.50000
0.50000 0.50000 -0.50000 -0.50000
0.70711 -0.70711 0.00000 0.00000
0.00000 0.00000 0.70711 -0.70711
and for N=8 it is
0.35355 0.35355 0.35355 0.35355 0.35355 0.35355 0.35355 0.35355
0.35355 0.35355 0.35355 0.35355 -0.35355 -0.35355 -0.35355 -0.35355
0.50000 0.50000 -0.50000 -0.50000 0.00000 0.00000 0.00000 0.00000
0.00000 0.00000 0.00000 0.00000 0.50000 0.50000 -0.50000 -0.50000
0.70711 -0.70711 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000
0.00000 0.00000 0.70711 -0.70711 0.00000 0.00000 0.00000 0.00000
0.00000 0.00000 0.00000 0.00000 0.70711 -0.70711 0.00000 0.00000
0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.70711 -0.70711
The last four rows are consecutive 2-shifts and the two and third rows are 4-shifts of each other. This a general fact that extends to higher dimensions and it is coherent with cascade algorithm. Implementing this idea, the computation of matrix can be sped up largely.

For D4 with N=4, the matrix is

0.48296 0.83652 0.22414 -0.12941
0.22414 -0.12941 0.48296 0.83652
-0.12941 -0.22414 0.83652 -0.48296
0.83652 -0.48296 -0.12941 -0.22414
The sum of the elements of each one of the two first rows is square root of 2 while for the two last rows the sum is zero. This is related to the fact that the former correspond to the scaling function and the latter to the wavelets.

The matrix for D4 with N=4 is

0.20425 0.42075 0.51226 0.63726 0.29575 0.07925 -0.01226 -0.13726
0.29575 0.07925 -0.01226 -0.13726 0.20425 0.42075 0.51226 0.63726
-0.17075 -0.04575 -0.13726 -0.17075 0.35377 0.72877 -0.04575 -0.51226
0.35377 0.72877 -0.04575 -0.51226 -0.17075 -0.04575 -0.13726 -0.17075
-0.12941 -0.22414 0.83652 -0.48296 0.00000 0.00000 0.00000 0.00000
0.00000 0.00000 -0.12941 -0.22414 0.83652 -0.48296 0.00000 0.00000
0.00000 0.00000 0.00000 0.00000 -0.12941 -0.22414 0.83652 -0.48296
0.83652 -0.48296 0.00000 0.00000 0.00000 0.00000 -0.12941 -0.22414
Now the elements of the two first rows add 2 and for the rest of the rows the sum is zero. Note again the same structure of the rows and that in the last half of rows there are zeros completing the length of the filter.

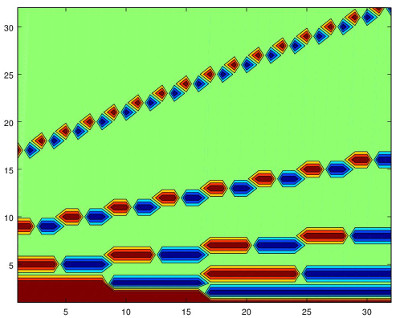
To visualize the situation in higher dimensions, let us consider a contour plot of the matrix for N=32. Dark blue are small values and dark red large values and the number of levels is 6. To prevent the large values of the last rows to mask other values, we normalize each row dividing by the maximum absolute value. In this way, every entry has absolute value at most 1 and each row contains a 1 or -1.

This is the result for the Haar filter:

image

The last rows (second coordinate large) correspond to the upper part. There are 5 levels of ’self-similarity’. The last one with horizontal bands covering one half of the width (imagine that the lower thin line coming from the first row is not there).

For the D4 filter we observe a funnier contour plot:

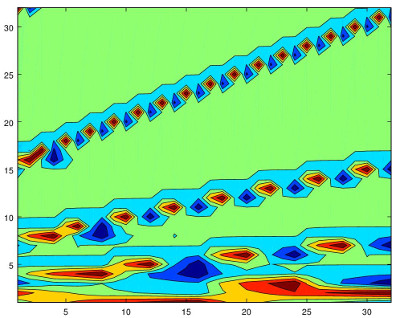image

The different scales of shifted wavelets correspond according to the cascade algorithm to the rows (2,4], (4,8], (8,16] and (16, 32] but the ’self-similarity’ is more difficult to appreciate.

To show that the first rows have a different behavior because they correspond to the scaling function, let us consider the filter D12. Its length is 12 and then we have 8 rows, the least power of two less than 12, giving approximations of shifts of the scaling function. Note that this is reflected in the contour plot:

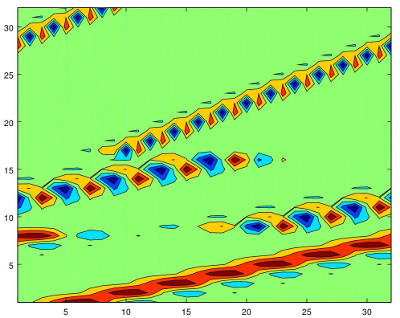image

Just for your curiosity, if we do not normalize the rows, the last contour plot becomes

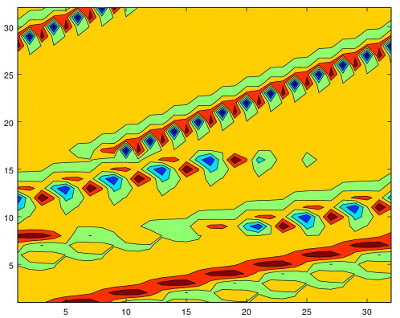image

Note that we have lost levels in the lower part because the large values in the upper part force to spread them out.


The code

This is octave code that produces the matrices and the figures:

pkg load signal

clear all
%close all

% Haar
haar = [1,-1]/sqrt(2);

% D4
fd4 = [ 1-sqrt(3), sqrt(3)-3, 3+sqrt(3), -1-sqrt(3)]/4/sqrt(2);

% D12 (the bizarre ordering compensated by fliplr is to copy the data from wikipedia)
fd12 = [0.15774243 , 0.69950381 ,1.06226376 , 0.44583132, -0.31998660, -0.18351806 , 0.13788809 , 0.03892321 , -0.04466375 , 7.83251152e-4, 6.75606236e-3, -1.52353381e-3 ];
fd12 = -fliplr(fd12)/sqrt(2).*(-1).^[1:size(fd12,2)];

% SINGLE MATRICES
disp('---Haar N=4---')
disp(wav_tr( haar, eye(4)))

disp('---Haar N=8---')
disp(wav_tr( haar, eye(8)))

disp('---D4 N=4---')
disp(wav_tr( fd4, eye(4)) )

disp('---D4 N=8---')
disp(wav_tr( fd4, eye(8)) )


% NORMALIZED MATRIX OF THE DWT
N = 32
lev = 6
W2 = wav_tr( haar, eye(N));
W4 = wav_tr( fd4, eye(N));
W12 = wav_tr( fd12, eye(N));
W2n = diag(1./max(abs(W2')))*W2;
W4n = diag(1./max(abs(W4')))*W4;
W12n = diag(1./max(abs(W12')))*W12;

% CONTOUR PLOTS
figure(1)
colormap ("default");
contourf (W2n, lev)
print -djpg file1.jpg

figure(2)
colormap ("default");
contourf (W4n, lev)
print -djpg file2.jpg

figure(3)
colormap ("default");
contourf (W12n, lev)
print -djpg file3.jpg

figure(4)
colormap ("default");
contourf (W12, lev)
print -djpg file4.jpg

The functions that compute the matrix of the DWT are (recall the disclaimer):

wav_tr

 wav_tr_m
% Wavelet transform: f=filter x=signal

function y = wav_tr(f,x)
  
  nx = size(x,1);
  Lf = size(f,2);
  Lc = nx;
  y = x;
  
  while Lc >= Lf
    y(1:Lc, :) = wav_tr_m( f, y(1:Lc, :));
    Lc = Lc/2;
  end
  
end
% Wavelet transform: f=filter x=signal

function y = wav_tr_m(f,x)
  
  nx = size(x,1);
  Lf = size(f,2);
  
  ro = zeros(1, nx);
  ro(1:Lf) = f;
  
  F = ro;
  for j= 2:nx/2
    F = [F; circshift(ro, [0,2*j-2])];
  endfor
  
  
  f = fliplr(f).*(-1).^[1:Lf];
  ro(1:Lf) = f;
  
  Fp = ro;
  for j= 2:nx/2
    Fp = [Fp; circshift(ro, [0,2*j-2])];
  end

  
  y = [Fp;F]*x;
  
end