The finite wavelet expansion

Any vector \(\vec{x}\in\mathbb{C}^N\) with \(N\) a power of 2 has a finite wavelet expansion. With the notation of my signal processing notes we have \[\vec{x} = \sum_{j=1}^N \lambda_j\vec{W}_j \qquad\text{where } \vec{W}_j=W^{-1}(\vec{e}_j), \quad \lambda_j=\vec{W}_j\cdot \vec{x}\] and \(W\) is the \(N\times N\) matrix of the corresponding wavelet transform.

The last \(N/2\) coefficients \(\lambda_j\) embody the finer details, the last level in the finite multiresolution analysis. The last \(N/2+N/4\) coefficients involve a level more and so on. In general to suppress the last \(L\) levels we have to replace the last \(M= (1-2^{-L})N\) coefficients by zeros. Let us call this operation \(Z_M\). In the reconstruction \[\vec{x}\longmapsto W^tZ_M\big(W\vec{x}\big)\] we should lose the detail corresponding to \(L\) levels.

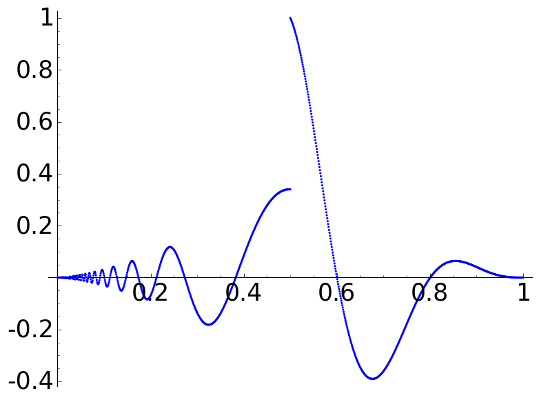
In this example we take for \(N=1024\) the signal \(\vec{x}\) given by \[x_j= \begin{cases} t_j^{3/2}\cos\big( 3/t_j\big)& \text{if } t_j\in [0,1/2), \\ 4(1-t_j)^{2}\sin (5\pi t_j)& \text{if } t_j\in [1/2,1), \end{cases}\] with \(t_j=j/N\), \(0\le j<N\).

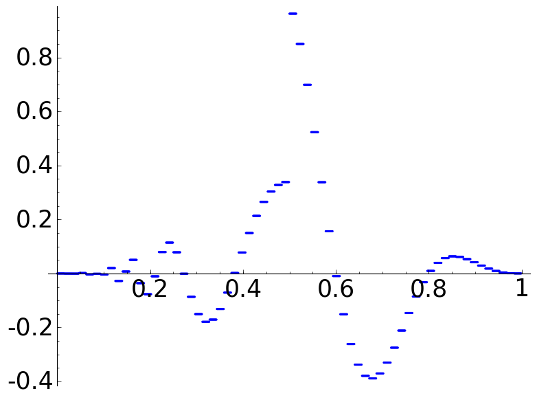
The aspect of the signal is like this:

fwe_0
The original signal

We are going to see the effect of the reconstruction when we use different values of \(L\) and different wavelet transforms. The calculations were done with Octave with the code below and the output was plotted with this sage plotter.


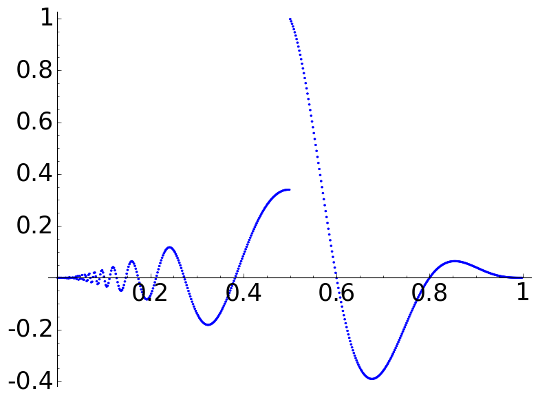
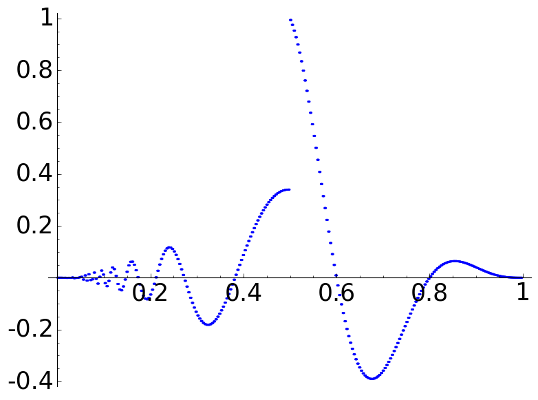
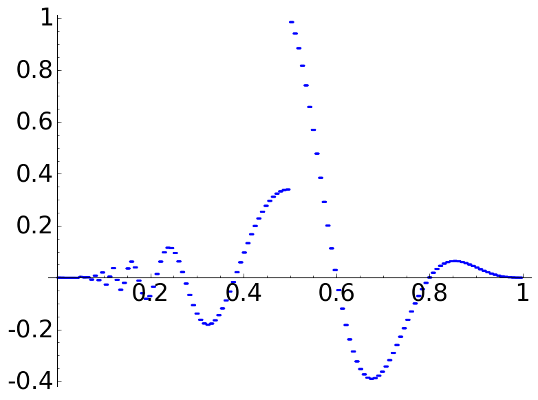
The most simple case is the Haar transform. The effect is just transforming the values of the signal into wider and wider steps.


D2_1 D2_2
D2 (Haar),   \(L=1\)
D2 (Haar),   \(L=2\)


D2_3 D2_4
D2 (Haar),   \(L=3\)
D2 (Haar),   \(L=4\)

The response at the discontinuity is good but the overall aspect is not very exciting.


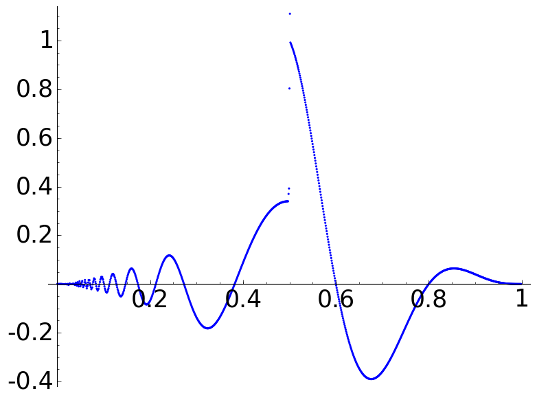
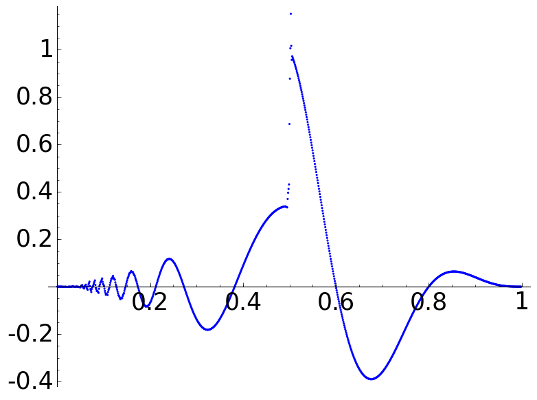
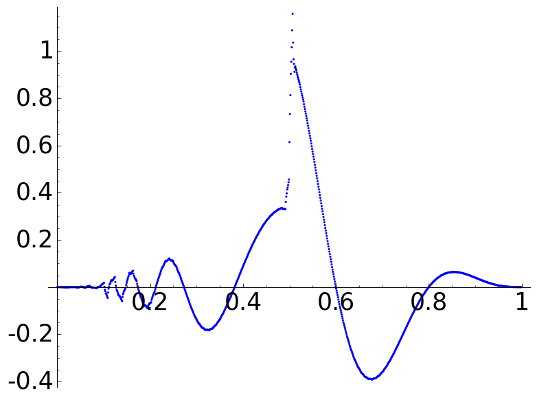
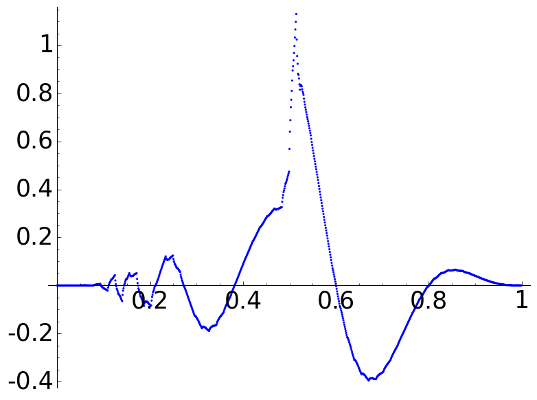
With D4 we obtain


D4_1 D4_2
D4,   \(L=1\)
D4,   \(L=2\)


D4_3 D4_4
D4,   \(L=3\)
D4,   \(L=4\)

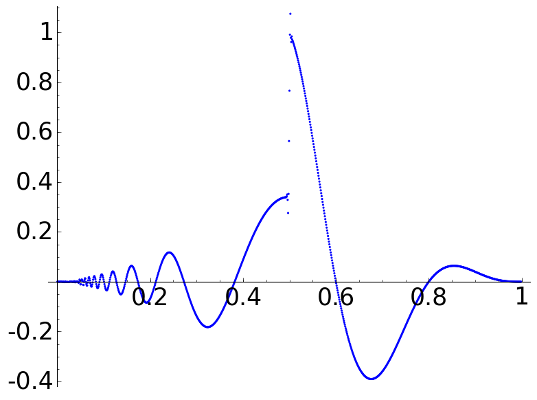
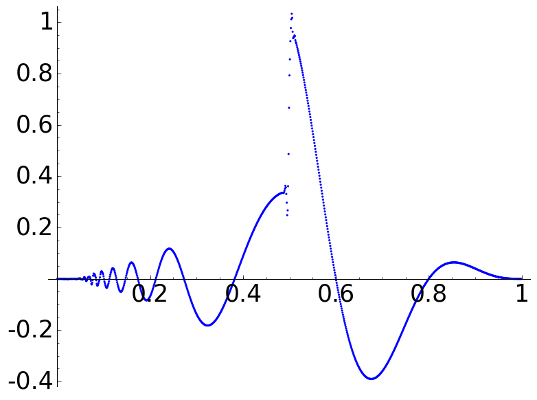
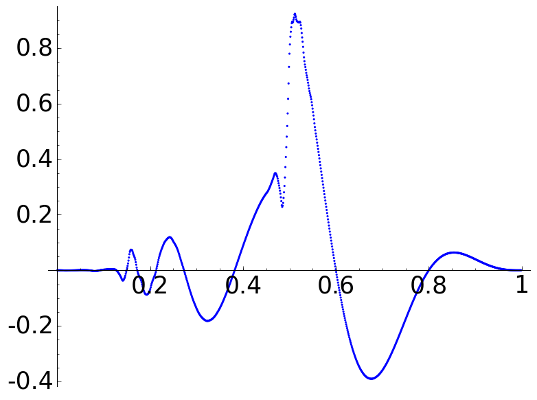
Finally with D8, we obtain


D8_1 D8_2
D8,   \(L=1\)
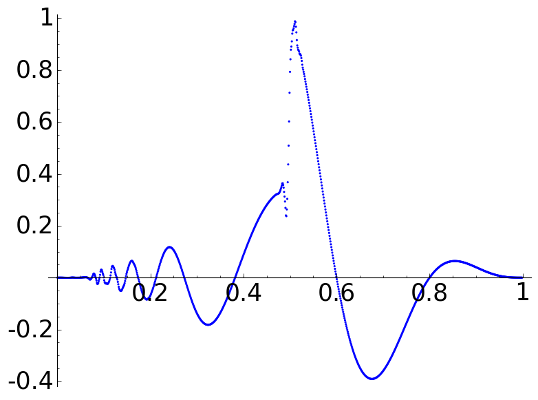
D8,   \(L=2\)


D8_3 D8_4
D8,   \(L=3\)
D8,   \(L=4\)


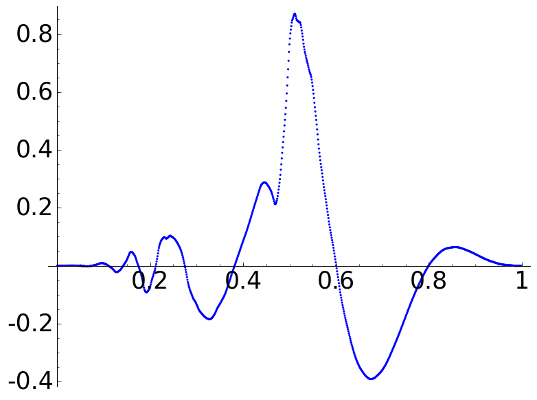
In the previous cases with \(L=5\) we would get quite bad results but with D8 we obtain something reflecting somewhat the global aspect:

fwe_0
D8,   \(L=5\)



The code

The octave code for the calculations:



% FINITE WAVELET EXPANSION

% sage_plotter.sage
% wav_tr.m
% wav_tr_m.m

pkg load signal

clear all


filename = "data_plot.txt";
fid = fopen (filename, "w");


% D4
fd4 = [ 1-sqrt(3), sqrt(3)-3, 3+sqrt(3), -1-sqrt(3)]/4/sqrt(2);

% D6
fd6 = [0.47046721, 1.14111692 , 0.650365, -0.19093442, -0.12083221, 0.0498175 ];
fd6 = -fliplr(fd6)/sqrt(2).*(-1).^[1:size(fd6,2)];

% D8
fd8 = [0.32580343 , 1.01094572 , 0.89220014, -0.03957503 , -0.26450717 , 0.0436163 , 0.0465036, -0.01498699];
fd8 = -fliplr(fd8)/sqrt(2).*(-1).^[1:size(fd8,2)];

% D12
fd12 = [0.15774243 , 0.69950381 ,1.06226376 , 0.44583132, -0.31998660, -0.18351806 , 0.13788809 , 0.03892321 , -0.04466375 , 7.83251152e-4, 6.75606236e-3, -1.52353381e-3 ];
fd12 = -fliplr(fd12)/sqrt(2).*(-1).^[1:size(fd12,2)];

% Haar
haar = [1,-1]/sqrt(2);



% SIGNAL
N = 1024
t = ( [0:N-1]/N )';
x = t.^1.5.*cos(3./t).*(t<1/2);
x(1)=0;
x += (t>=0.5).*sin(5*pi*t)*4.*(1-t).^2;

% MATRICES OF THE TRANSFORMS
W2 = wav_tr( haar, eye(N));
W4 = wav_tr( fd4, eye(N));
W8 = wav_tr( fd8, eye(N));


% PLOT SIGNAL x

fprintf (fid, '(%f, %f)\n', [linspace(0,1/2,N/2); x(1:N/2)']);
fprintf (fid, '>!_!_!_\nPJ0 SI5\n!_!_!_<\n');

fprintf (fid, '(%f, %f)\n', [linspace(1/2,1,N/2); x(N/2+1:N)']);
fprintf (fid, '>!_!_!_\nPJ0 SI5 FI../images/fwe_0.png\n!_!_!_<\n');

W = W2; % Haar
for L = 1:4
  y = W*x;
  M = (2^L-1)*N/2^L;
  y( N-M+1: N) = zeros(M,1);
  fprintf (fid, '(%f, %f)\n', [t'; (W'*y)']);
  metadat = '>!_!_!_\nPJ0 SI5 FI../images/fwe_D2_%d.png\n!_!_!_<\n';
  fprintf (fid, sprintf(metadat,L));
end

W = W4; % D4
for L = 1:4
  y = W*x;
  M = (2^L-1)*N/2^L;
  y( N-M+1: N) = zeros(M,1);
  fprintf (fid, '(%f, %f)\n', [t'; (W'*y)']);
  metadat = '>!_!_!_\nPJ0 SI5 FI../images/fwe_D4_%d.png\n!_!_!_<\n';
  fprintf (fid, sprintf(metadat,L));
end

W = W8; % D8
for L = 1:5
  y = W*x;
  M = (2^L-1)*N/2^L;
  y( N-M+1: N) = zeros(M,1);
  fprintf (fid, '(%f, %f)\n', [t'; (W'*y)']);
  metadat = '>!_!_!_\nPJ0 SI5 FI../images/fwe_D8_%d.png\n!_!_!_<\n';
  fprintf (fid, sprintf(metadat,L));
end


fclose (fid);



It calls to two functions:


File wav_tr.m File wav_tr_m.m
% Wavelet transform: f=filter x=signal

function y = wav_tr(f,x)
  
  nx = size(x,1);
  Lf = size(f,2);
  Lc = nx;
  y = x;
  
  while Lc >= Lf
    y(1:Lc, :) = wav_tr_m( f, y(1:Lc, :));
    Lc = Lc/2;
  end
  
end
% Wavelet transform: f=filter x=signal

function y = wav_tr_m(f,x)
  
  nx = size(x,1);
  Lf = size(f,2);
  
  ro = zeros(1, nx);
  ro(1:Lf) = f;
  
  F = ro;
  for j= 2:nx/2
    F = [F; circshift(ro, [0,2*j-2])];
  endfor
  
  
  f = fliplr(f).*(-1).^[1:Lf];
  ro(1:Lf) = f;
  
  Fp = ro;
  for j= 2:nx/2
    Fp = [Fp; circshift(ro, [0,2*j-2])];
  end

  
  y = [Fp;F]*x;
  
end