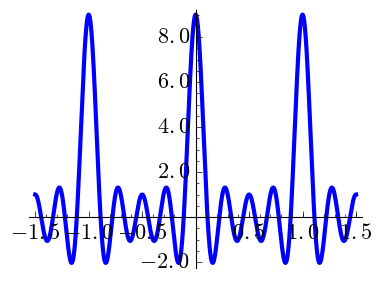
The Dirichlet kernel \[D_N(x) = \sum_{n=-N}^N e(nx)\] has a pivotal importance when studying Fourier series. In some sense it is an approximation of the 1-periodic Dirac delta when \(N\to \infty\). The slow decay is an issue when one enters into convergence problems.
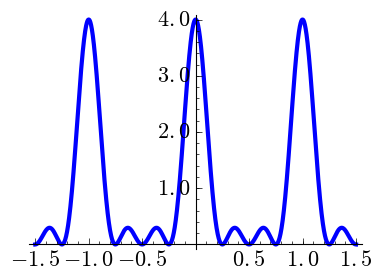
A more regular version is the Fejér kernel, which is the Cesàro sum of the Dirichlet kernel except for shifting \(N\) into \(N-1\), \[F_N(x) = \sum_{n=-N}^N \Big( 1-\frac{|n|}{N} \Big) \exp(2\pi i nx)\] The quickest decay of this function at the cost of having thicker peaks (this also appears in digital windows) allows to prove a nice theorem (Fejér's theorem): If \(f\) is 1-periodic and continuous having \(\{a_m\}_{m\in\mathbb{Z}}\) as Fourier coefficients, then \[f(x)=\lim_{N\to \infty} \sum_{m=-N}^N \Big( 1-\frac{|m|}{N} \Big) a_m\exp(2\pi i mx) \qquad \text{uniformly in }x.\]
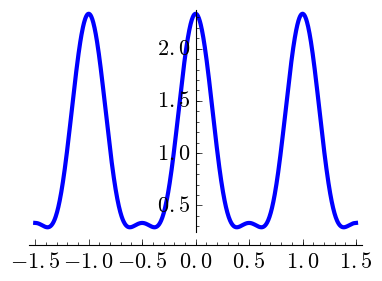
One may consider smoother versions, so to speak, of the Dirichlet kernel taking higher Cesàro sums. The natural object for \(k\) a nonnegative integer is \[C_{N,k}(x) = \sum_{n=-(N-k)}^{N-k} \binom{N-k}{|n|} \binom{N}{|n|}^{-1} \exp(2\pi i nx).\] Note that \[D_N(x)= C_{N,0}(x) \qquad\text{and}\qquad F_N(x)= C_{N,1}(x).\]
The following plots drawn with the code below show the cases \(k=0,1,2\) for some small values of \(N\).
 |
 |
 |
| \(N=4,\) \(k=0\) | \(N=4,\) \(k=1\) | \(N=4,\) \(k=2\) |
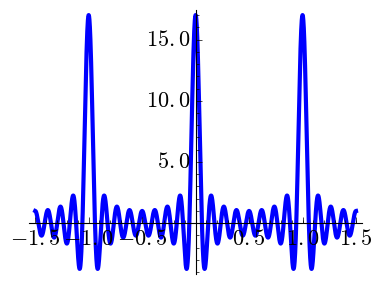 |
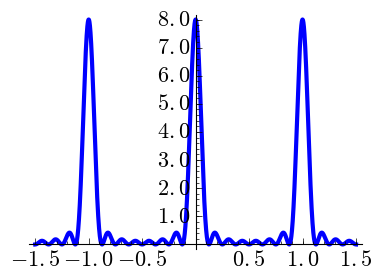 |
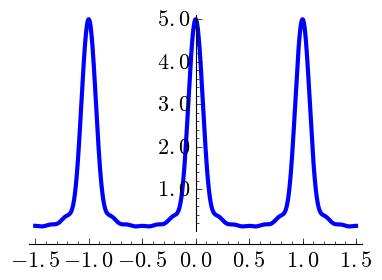 |
| \(N=8,\) \(k=0\) | \(N=8,\) \(k=1\) | \(N=8,\) \(k=2\) |
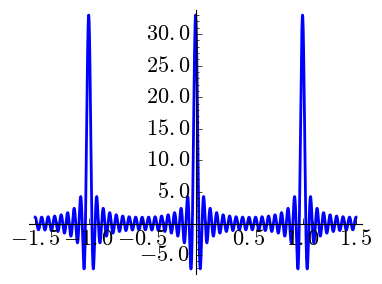 |
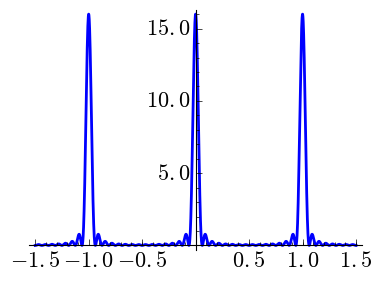 |
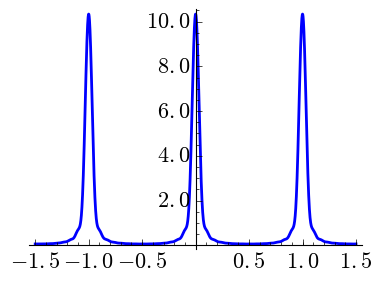 |
| \(N=16,\) \(k=0\) | \(N=16,\) \(k=1\) | \(N=16,\) \(k=2\) |
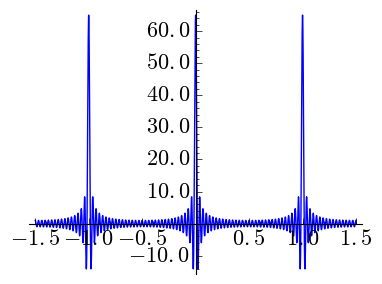 |
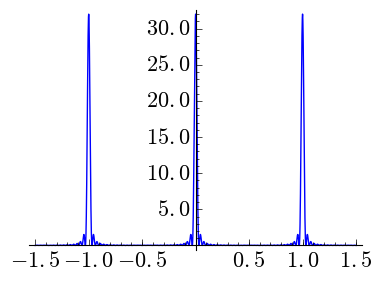 |
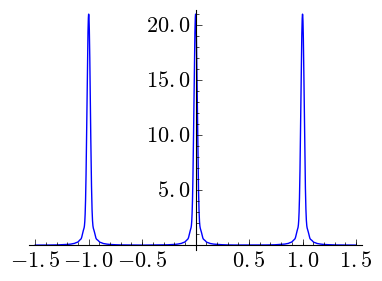 |
| \(N=32,\) \(k=0\) | \(N=32,\) \(k=1\) | \(N=32,\) \(k=2\) |
It is interesting to observe the vertical scale. When \(k\) grows the peaks are shorter and wider. Note that \(\int_{-1/2}^{1/2}C_{N,k}=1\) as it must be if we want to mimic a Dirac delta.
|