Digital windows


Mathematically the windows used in digital signal processing to construct FIR filters are trigonometrical polynomials \[f(x) = \sum_{k=-N}^N w_k e^{2\pi i kx}\] such that \(f\) in \(I=[-1/2,1/2]\) mimics in some way a Dirac delta at the origin: a big thin peak and a quick decay under the normalization \(\int_I f=1\).

The natural choice is \(w_k=1\), called the rectangular window. Its peak is the thinnest but it decays only like \(N/x\). The triangular window is the Fejér kernel \(w_k=(1-|k|/N)_+\), very interesting in the theory of Fourier series but not used in practice because the width of the peak can be reduced and the decay improved. Some common alternatives are:

The Hann window \[w_k= \frac{1}{2} + \frac{1}{2}\cos\frac{\pi k}{N},\] the Hamming window \[w_k= w_k= \frac{25}{46} + \frac{21}{46}\cos\frac{\pi k}{N}\] and the Blackman window \[w_k= \frac{3969}{9304} + \frac{1155}{2326} \cos\frac{\pi k}{N} + \frac{715}{9304} \cos\frac{2\pi k}{N}\] where the funny coefficients are very often approximated by \(21/50\), \(1/2\) and \(2/25\).

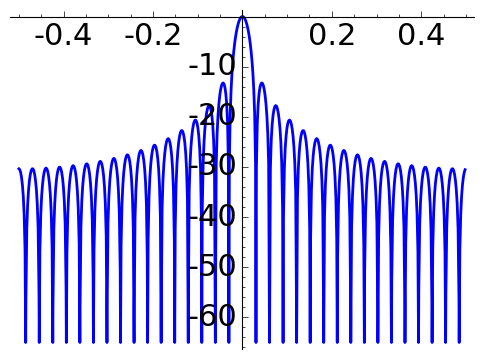
In engineering, the quality of a window is measured studying the width of the main lobe and the size of the peak side lobe in the attenuation in decibels \[A(x)= 20\log_{10}\Big|\frac{f(x)}{f(0)}\Big|.\]

The following plots of \(A\) for \(N=16\) are obtained with the code below.



rect
Rectangular window




tria
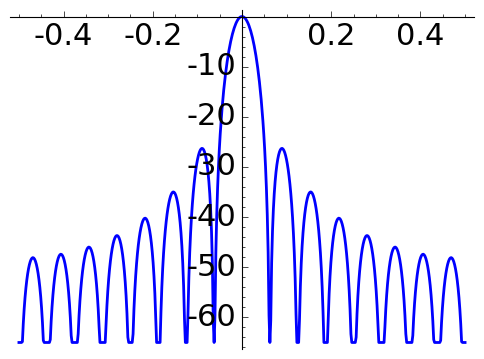Triangular window




hann
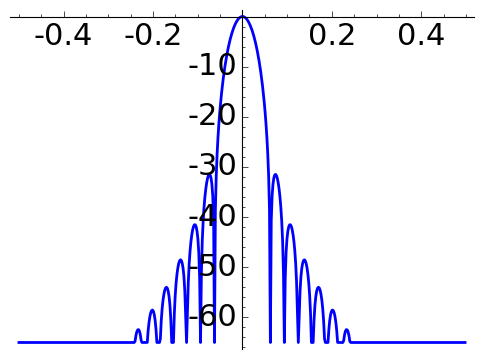Hann window




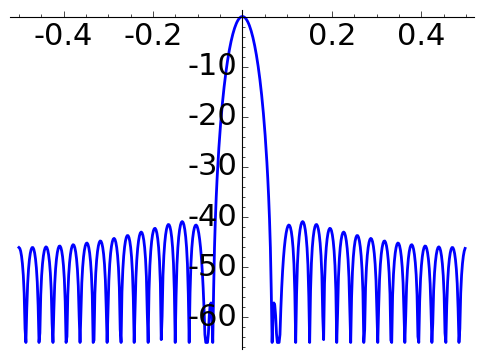hamming
Hamming window




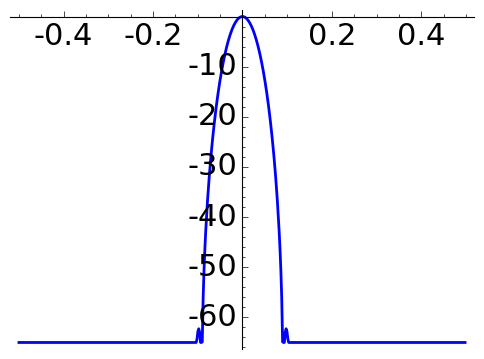black
Blackman window




The code

This is the SAGE code for all the  images. The rectangular and triangular windows have special definitions to show fully the vertical lines.


N = 16
db_low = -65
np = 512

thi = 2

def plot_win(LW, c='blue'):
  L_to_plot = []
  temp = []
  for xp in srange(-1/2,1/2,1/np):
    S = LW[0]
    for k in srange(1,N+1):
      S += ( 2*LW[k]*cos(2*pi*k*xp) ).n()
    temp.append( abs(S) )
  k = 0
  m = max(temp)
  for xp in srange(-1/2,1/2,1/np):
    y = temp[k]/m+10^(2*db_low)
    y = max(20*log(y)/log(10),db_low)
    L_to_plot.append( (xp,y) )
    k += 1
  return list_plot(L_to_plot, plotjoined=True, color=c, thickness=thi)


def plot_winrect(c='blue'):
  L_to_plot = []
  temp = []
  for xp in srange(-1/2,1/2,1/np):
    if xp==0:
      temp.append( 1 )
    else:
      S = sin(pi*(2*N+1)*xp)/sin(pi*xp)/(2*N+1)
      temp.append( abs(S) )
  k = 0
  for xp in srange(-1/2,1/2,1/np):
    y = temp[k]+10^(2*db_low)
    y = max(20*log(y)/log(10),db_low)
    L_to_plot.append( (xp,y) )
    k += 1
  for k in srange(-N,N+1):
    if k!=0:
      L_to_plot.append( (k/(2*N+1),db_low) )
  L_to_plot.sort()
  return list_plot(L_to_plot, plotjoined=True, color=c, thickness=thi)


def plot_wintria(c='blue'):
  L_to_plot = []
  temp = []
  for xp in srange(-1/2,1/2,1/np):
    if xp==0:
      temp.append( 1 )
    else:
      S = (sin(pi*N*xp)/sin(pi*xp)/N)^2
      temp.append( abs(S) )
  k = 0
  for xp in srange(-1/2,1/2,1/np):
    y = temp[k]+10^(2*db_low)
    y = max(20*log(y)/log(10),db_low)
    L_to_plot.append( (xp,y) )
    k += 1
  for k in srange(-N,N+1):
    if k!=0 and abs(k)<=N/2:
      L_to_plot.append( (k/N,db_low) )
  L_to_plot.sort()
  return list_plot(L_to_plot, plotjoined=True, color=c, thickness=thi)

  

def rectw():
  LW = (N+1)*[1]
  return LW
  
def triaw():
  LW = []
  for k in srange(N+1):
    LW.append( 1-k/N )
  return LW
  

def hannw():
  a0 = 1/2
  LW = []
  for k in srange(N+1):
    LW.append( a0+(1-a0)*cos(pi*k/N) )
  return LW
  
def hammw():
  a0 = 25/46
  LW = []
  for k in srange(N+1):
    LW.append( a0+(1-a0)*cos(pi*k/N) )
  return LW
  
def blacw():
  a0 = 7938/18608
  a1 = 9240/18608
  a2 = 1430/18608
  LW = []
  for k in srange(N+1):
    LW.append( a0+a1*cos(pi*k/N)+a2*cos(2*pi*k/N) )
  return LW
  
def kaiserw( al ):
  LW = []
  for k in srange(N+1):
    y = bessel_I( 0, al*sqrt(1-(k/N)^2) )/bessel_I(0, al)
    LW.append( y.n() )
  return LW
  
  
fs = 5
P = plot_winrect( )
# Better than plot_win( rectw() )
P.fontsize(22)
P.save('../images/w_rect.png', figsize=fs)


P = plot_wintria( )
# Better than plot_win( triaw() )
P.fontsize(22)
P.save('../images/w_tria.png', figsize=fs)

  
P = plot_win( hannw() )
P.fontsize(22)
P.save('../images/w_hann.png', figsize=fs)

    
P = plot_win( hammw() )
P.fontsize(22)
P.save('../images/w_hamm.png', figsize=fs)

    
P = plot_win( blacw() )
P.fontsize(22)
P.save('../images/w_black.png', figsize=fs)