Wigner's semicircle law

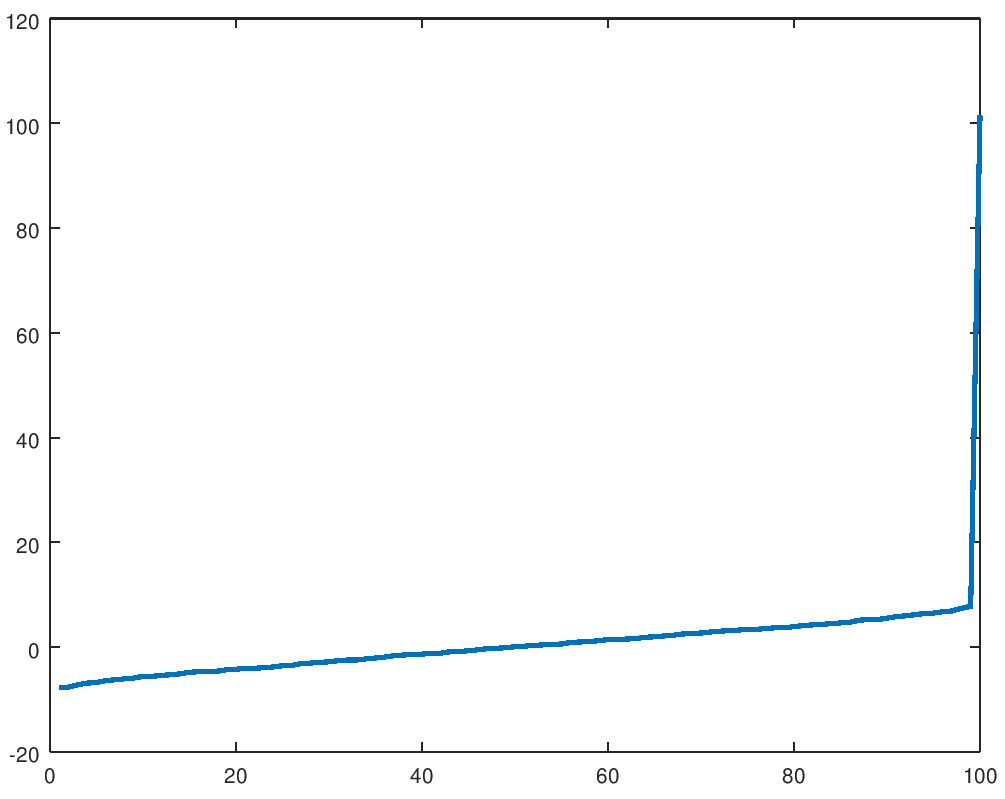
It seems natural that if we take a random \(n\times n\) symmetric matrix then the eigenvalues, which are generically \(n\) distinct real numbers, should be random as well. Some naive experiments with matlab/octave can surprise us revealing a strange form of randomness. For instance, if we try A = rand(100) and plot( eig(A+A') ) then we get typically a figure like this: Apparently there is a large dominating eigenvalue.

If we try simply plot( eig(A) ) to avoid any connection with the symmetry, we obtain something like this: Here the eigenvalues are generically complex but there a largely dominant eigenvalue that is close to be real.

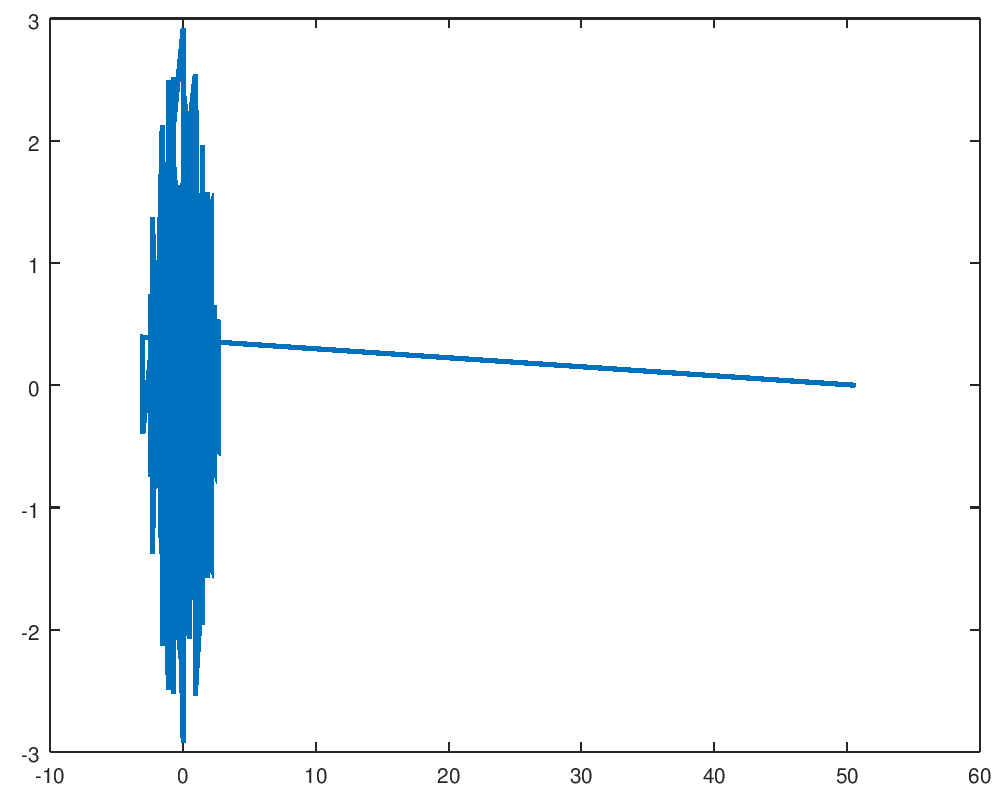The explanation is simple. The rand command generates pseudorandom numbers uniformly distributed in \((0,1)\). Then we can think that \(A=\frac{1}{2}\textbf{1}+B\) with \(\textbf{1}\) the matrix having all the entries one while the entries of \(B\) are evenly distributed in \((-1/2,1/2)\). With plot( eig(A-1/2*ones(100)) ) we check that \(B\) has the expected randomness: 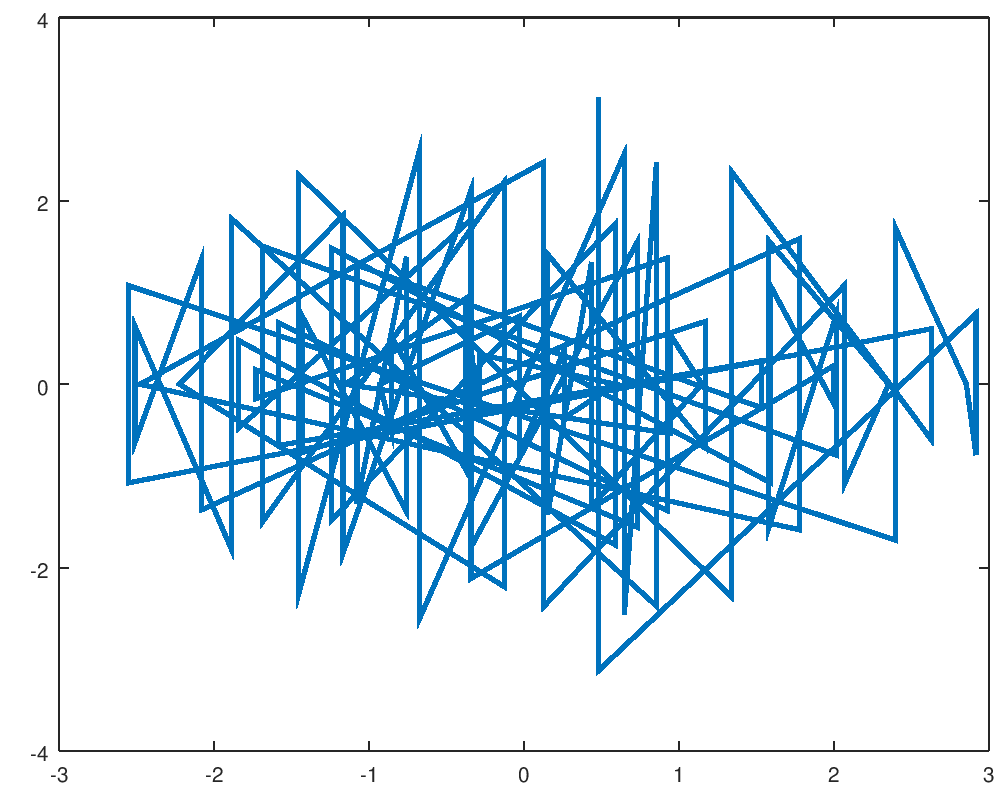The bias is introduced by \(\frac{1}{2}\textbf{1}\). This matrix has an eigenvalue 50 with multiplicity one, which corresponds to the eigenvector \(\vec{v}\) with coordinates equal to 1, and a zero eigenvalue with multiplicity 99, since the rank is one. We expect a lot of cancellation in \(B\vec{v}\) then \(\vec{v}\) is close to be an eigenvector of \(A\). In general, if \(A\) is a large \(n\times n\) matrix built with rand, we expect a large eigenvalue of size \(n/2\), in agreement with our previous experiments.

The loose end in the previous argument is that we are assuming that when the entries are uniformly distributed in \((-1/2,1/2)\) or, in general, in \((-a,a)\), the eigenvalues cannot be very large in comparison to \(n/2\) in the typical situations. The so called Wigner's semicircle law goes a step forward in the case of symmetric (or Hermitian) matrices and shows that under quite general conditions, there is a limiting distribution for the scaled eigenvalues. The usual proofs are based on computing the moments using the trace of powers of the matrix. This idea is in early works of E. P. Wigner who firstly stated a result of this kind (see for instance this for a more general mathematical statement). The plot of the density function of the limiting distribution is a semicircle after scaling (i.e., a semiellipse). By this reason, the probability distributions having this property are called Wigner semicircle distribution.

The matlab/octave code below creates a symmetric matrix with independent entries (except for the symmetry) uniformly distributed in \((-1,1)\) and plots the histogram of the eigenvalues conveniently scaled to fit in \([-1,1]\times [0,1]\). Running it we get figures like this:

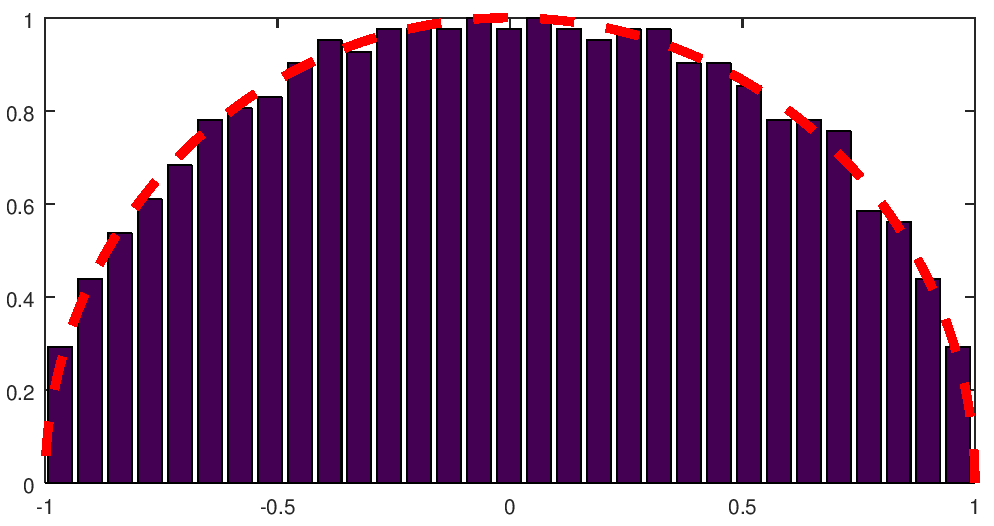N = 1000

To see the semicircle, the dimension must be large. Even 100 is too small, as the following figure shows. Other experiments with the same dimension give worse results.

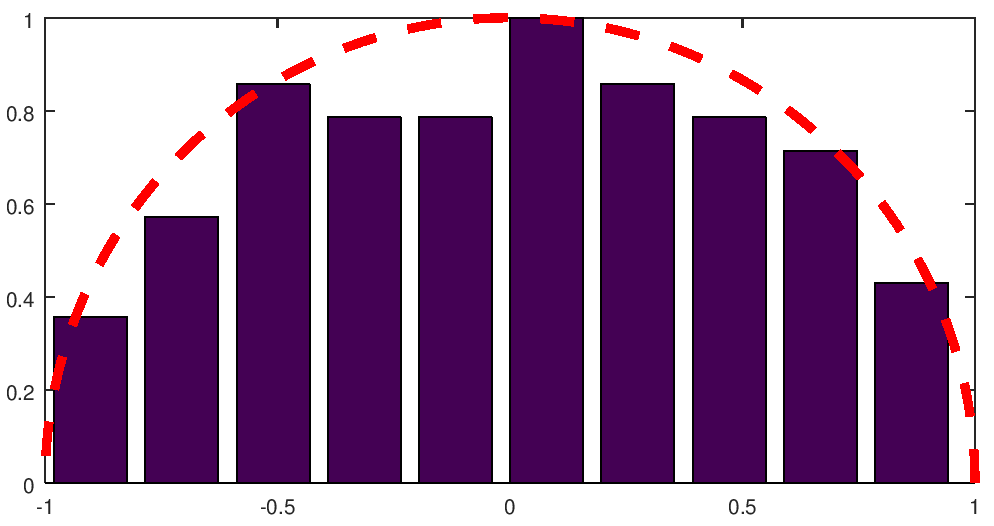N = 100

Increasing the dimension to 5000 and the number of bins as the square root, we do not see fundamental improvements.

N = 5000

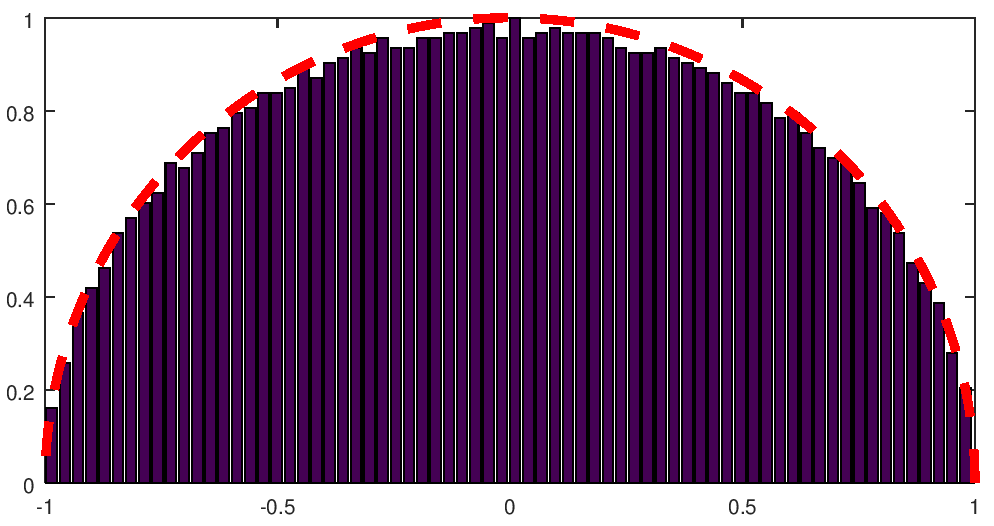For this dimension, it sounds reasonable to take less bins. In the following plot they are 40:

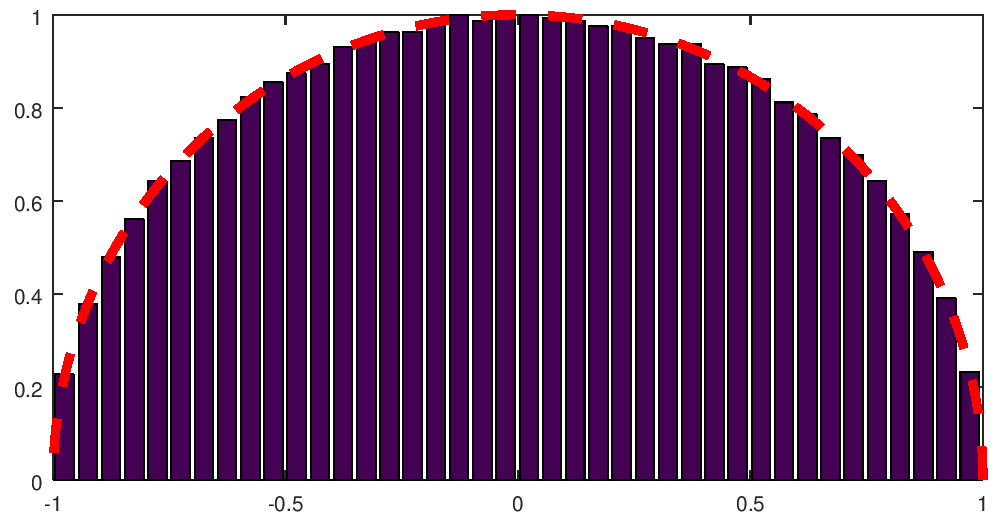N = 5000

The result does not depend on the distribution of the entries (under mild conditions). For instance, we could change the third line by A = randn(N), which use a standard Gaussian distribution, without any sensible effect.

The code