Sound quantization

1. First part

Let us start with something that actually is not a quantization of the signal although somebody could consider that it is a quantization of the sampling times. Let us assume that we have subsampled a signal under the requirements of the output device and instead of applying some kind of interpolation to create the missing values we repeat each value a number of times. The program generates a pure sine tone of 500Hz sampled to 44.1kHz and a signal of the same frequency repeating each value 4 times. When we open the result with audacity, we see

Clicking the following links you can (hopefully) hear how the first signal sounds and the same for the second signal. Do you note a strange pitch in the second?

2. Second part

The next experiment consists in the quantization of the amplitudes in a voice signal. The program below reduces the possible amplitudes to nr values, approximating by the closer level.
The plot with the program of the original voice is not very informative but it is fine to get a reference.

It sounds like this. (The original is taken from here.)

With only nr=8 admissible values we have

You see that the upper and lower levels are very seldom employed and the first guess is that something like probably is not understable but it sounds quite well given the lack of information like. Check this.

If we reduce nr=2, the mininum value corresponding to a sound, the previous figure would be a simple band. Using audacity to enlarge a portion on the signal, we obtain

But when we play it the result is not a buzz, the sentence is still understandable. It sounds like this.
The conclusion is that we perceive the meaning of the voice mainly with frequencies.

A last comment is that when the number of levels is odd the quality seems to decrease. For instance, this is the result for nr=3.

The code

The simple Matlab/Octave programs employed before have been:

% SUBSAMPLING

%number of repetitions (1 -> original)

nr = 4;

disp(['number of repetitions = ' num2str(nr)])

      

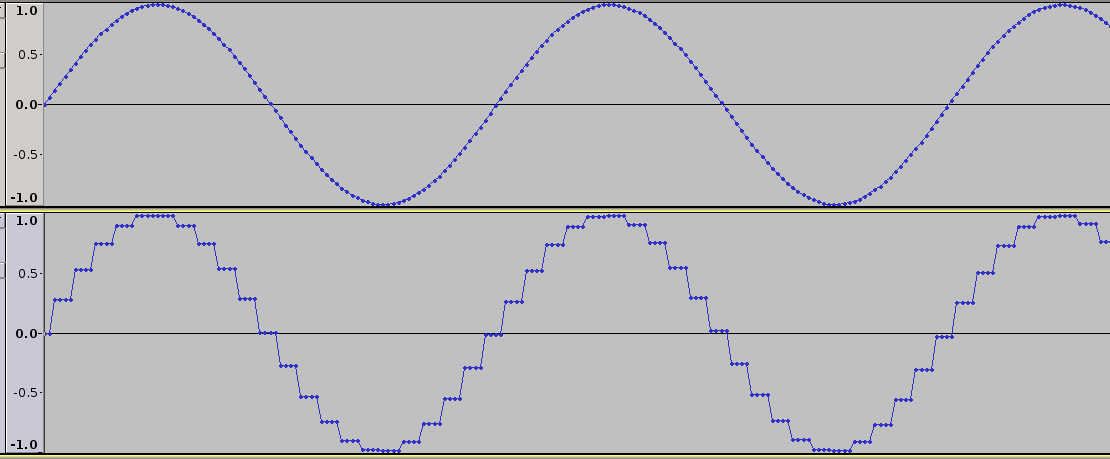
% efect of sampling change N and Fs

f = 500;

Fs = 44100;

T = 2; %duration

y = 0.1*0.99*sin(2*pi*f*linspace(0,1*T,Fs*T));

      

%total length

tl = size(y,2);

fprintf('Number of sampling points = %d\n',size(y,2));

      

y = [y,zeros(1,nr)];

y = y( nr*floor([0:tl-1]/nr+0.5)+1 );

      

sound(y, Fs)

%
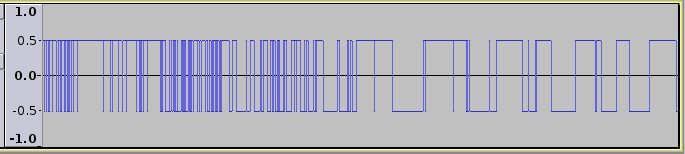
AMPLITUDE QUANTIZATION

%number of levels

nr = 2;

disp(['number of levels = ' num2str(nr)])

      

delt = 2/nr;

      

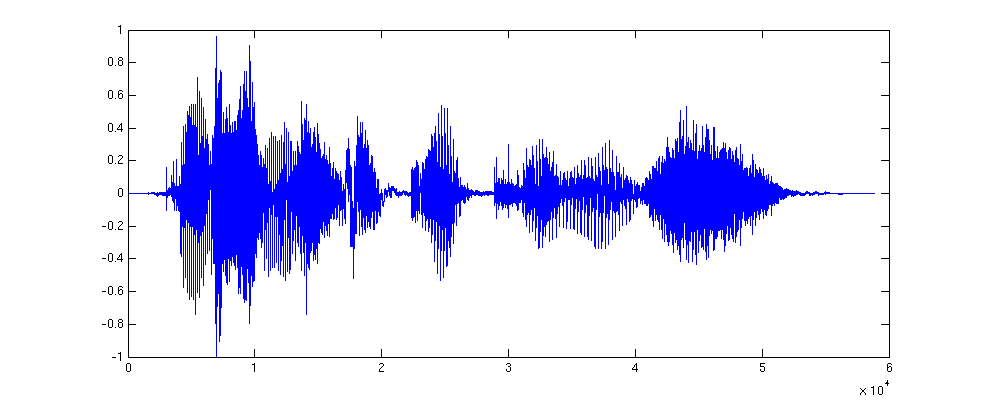
% Read file

filename = 'input.wav';

[y,Fs] = audioread(filename);

% stereo -> mono

y = y(:,1);

      

% adjust volume 

v = max( max(y),-min(y) );

y = y/v*0.999999;

      

figure(1)

plot(y)

      

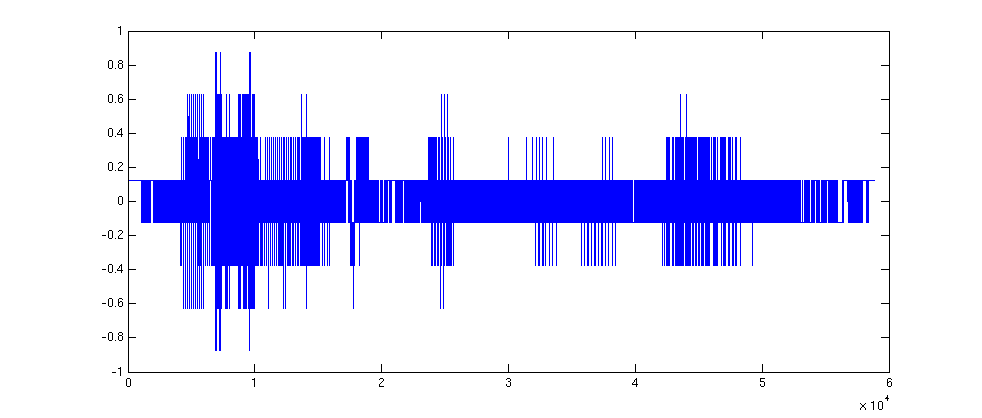
% quantize

y = delt*floor((y+1)/delt)+delt/2-1;

      

disp('The levels are:')

disp(unique(y))

      

figure(2)

plot(y)

      

sound(y,Fs)

audiowrite('OUTPUT.wav',y,Fs);