Following this paper by C. Aslangul, consider the quantum infinite potential well in \([0,1]\) with the \(N\)-th eigenstate as initial condition. After a sudden expansion to \([0,\Lambda]\), with \(\Lambda>1\), the evolution of the system is ruled by the Schrödinger equation \[\begin{cases} i\hbar \partial_t\Psi(x,t)= -\dfrac{\hbar^2}{2m}\partial_{xx}\Psi(x,t)\quad\text{for $0<x<\Lambda $}, \quad \text{$t>0$,} \\[6pt] \Psi(0,t)=\Psi(\Lambda ,t)=0,\quad \Psi(x,0)=\sqrt{2}\,\theta(1-x)\sin(N\pi x) \end{cases}\] where \(\theta(x)\) is the Heaviside step function taking the value \(1\) if \(x\ge 0\) and \(0\) if \(x<0\).
For \(a/q\) an irreducible fraction, define \(p:[0,1/2]\longrightarrow\mathbb{R}\) given by \[p(x) = 2\Lambda \Big|\Psi\big(2\Lambda x,\frac aq T\big)\Big|^2 \qquad\text{with}\quad T=\frac{4m\Lambda^2}{\pi \hbar}.\] This is the probability density corresponding to the fractional time \(aT/q\) when \([0,\Lambda]\) is normalized to \([0,1/2]\).
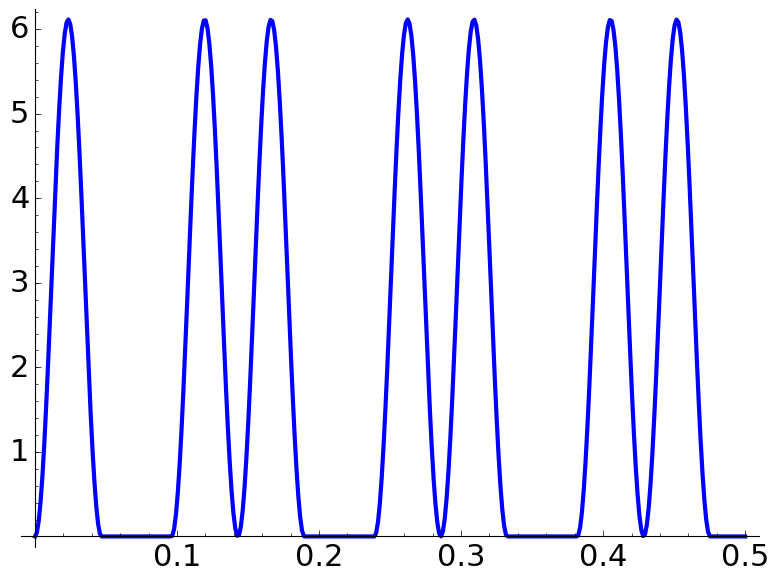
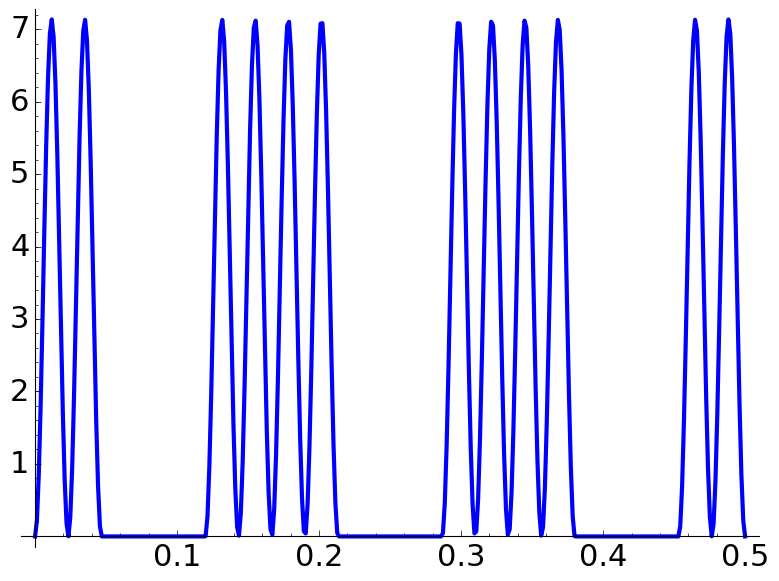
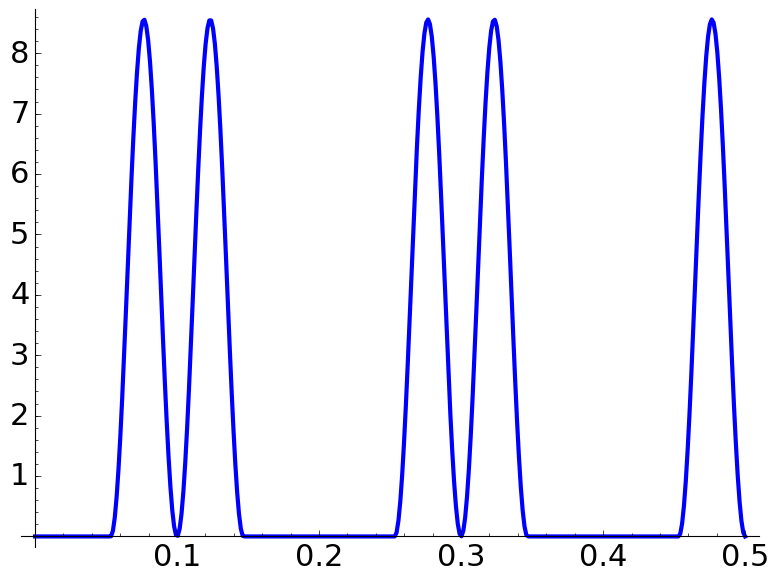
If \(\Lambda>q\) for \(q\) odd or \(\Lambda>q/2\) for \(q\) even the probability density "fragmentizes" into blocks of \(2N\) peaks (coming from the initial condition) separated by forbidden zones (\(0\)-level plateaux) of width \(q^{-1}-\Lambda^{-1}\) or \(2q^{-1}-\Lambda^{-1}\) depending on whether \(q\) is odd or even. The blocks in the extremes can be halved. If \(q\) is odd, there are \(qN\) peaks in total and if \(q\) is even, there are \(qN/2\).
These are some plots of \(p\) under these conditions choosing \(\Lambda=10.7\). All the figures in this document are produced with the sagemath code below. Full resolution versions are obtained clicking on the images.

|

|
 |
| \(\Lambda=10.7,\) \(\dfrac aq=\dfrac{2}{7},\) \(N=1\) | \(\Lambda=10.7,\) \(\dfrac aq=\dfrac{1}{12},\) \(N=2\) | \(\Lambda=10.7,\) \(\dfrac aq=\dfrac{3}{10},\) \(N=1\) |
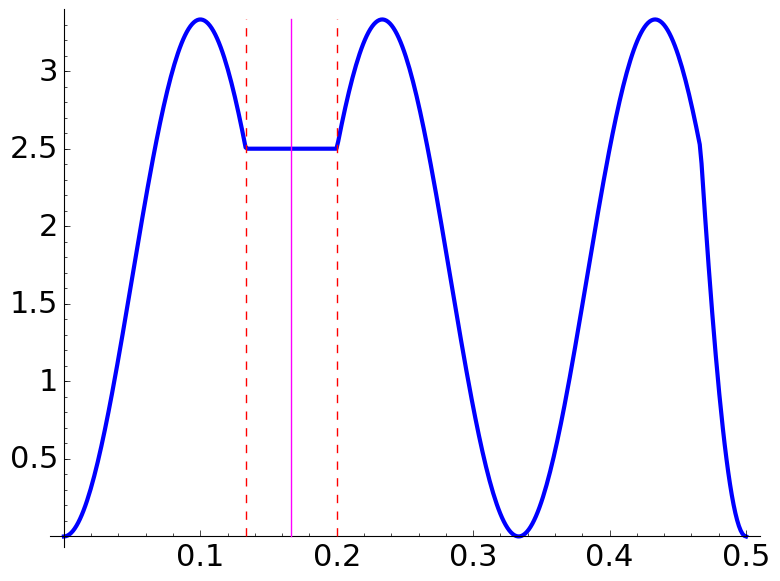
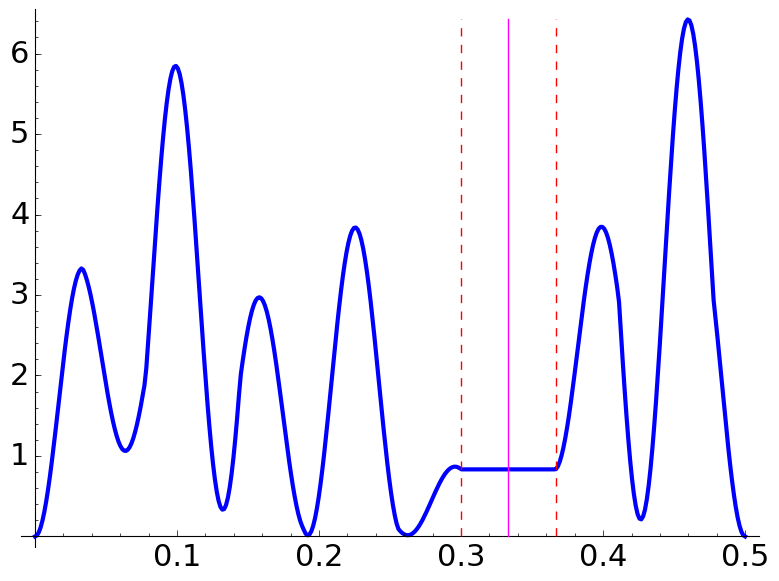
Now, consider the cases \(\Lambda<q\) when \(q\) is odd and \(\Lambda<q/2\) when \(q\) is even. If \(2N\Lambda\) is an odd integer, a plateau in the probability density \(p\) appears over the interval \[[c-r,c+r]\cap [0,1/2] \qquad\text{with}\quad c = \Big\langle\frac {2a}q N\Lambda+\frac 12\Big\rangle\] where \(\langle x\rangle\) is the function giving the distance to the nearest integer and \[r = \frac 1q\Big\langle\frac {q+\Lambda}{2\Lambda}\Big\rangle \quad\text{if }2\nmid q \qquad\text{and}\qquad r = \frac 2q\Big\langle\frac {q+2\Lambda}{4\Lambda}\Big\rangle \quad\text{if }2\mid q.\]
In the following examples, the center and the boundary of the plateaux are marked with vertical lines.
|
|
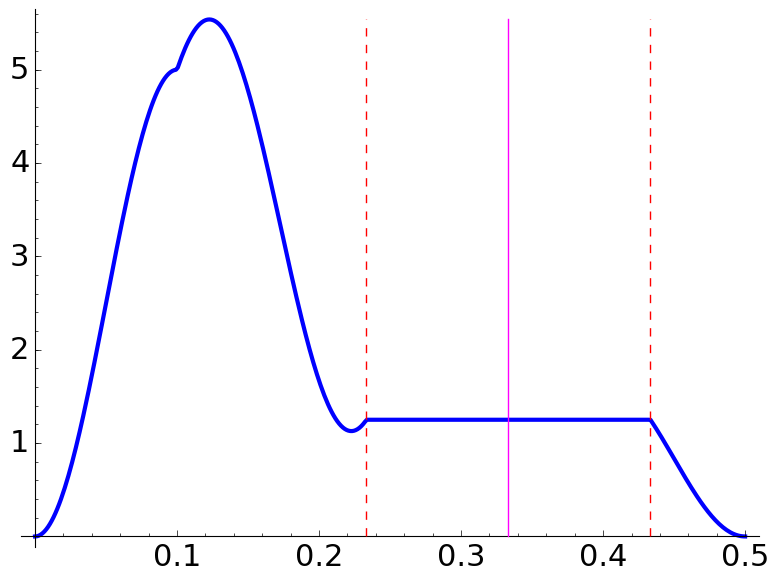 |
| \(\Lambda=\dfrac52,\) \(\dfrac aq=\dfrac{1}{3},\) \(N=1\) | \(\Lambda=\dfrac52,\) \(\dfrac aq=\dfrac{13}{18},\) \(N=3\) | \(\Lambda=\dfrac54,\) \(\dfrac aq=\dfrac{11}{6},\) \(N=2\) |
The intervals in which the plateaux appear are \([2/15,1/5]\), \([3/10,11/30]\) and \([7/30,13/30]\), respectively.
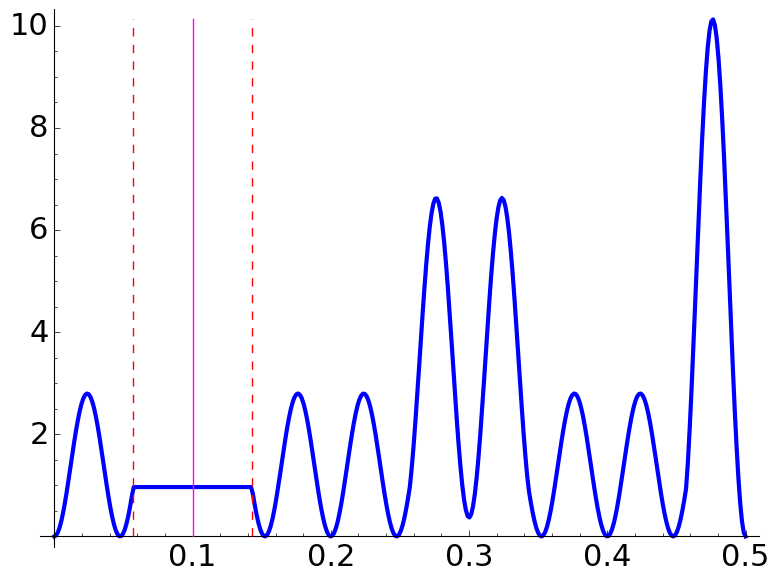
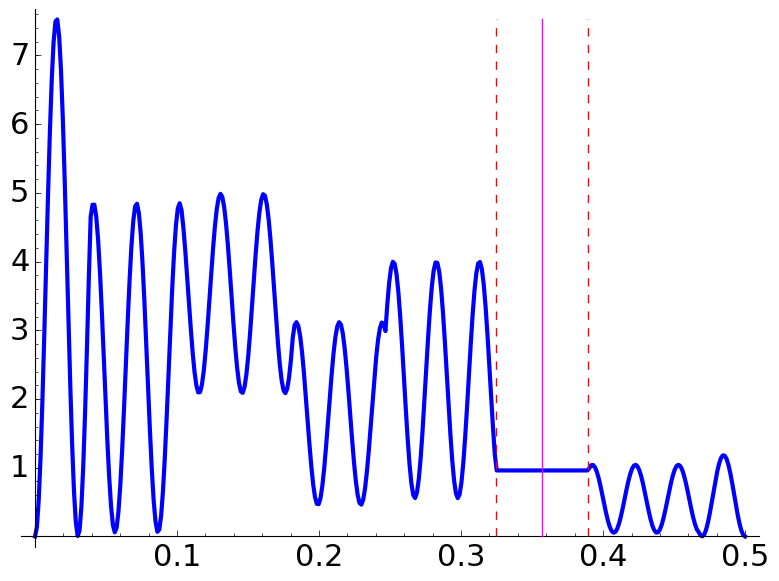
These are more examples exhibiting plateaux:
|
|
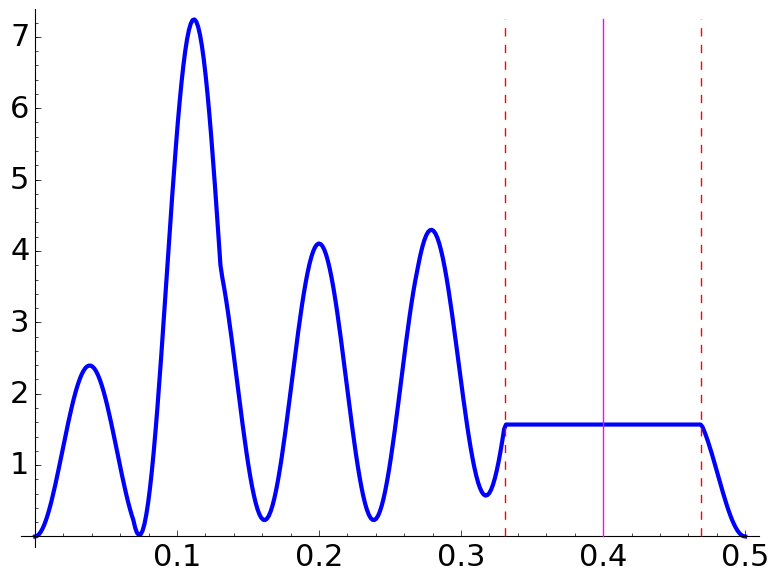 |
| \(\Lambda=\dfrac72,\) \(\dfrac aq=\dfrac{8}{5},\) \(N=3\) | \(\Lambda=\dfrac{11}{4},\) \(\dfrac aq=\dfrac{3}{7},\) \(N=6\) | \(\Lambda=\dfrac{13}{6},\) \(\dfrac aq=\dfrac{7}{10},\) \(N=3\) |
This time, the intervals are \([2/35,1/7]\), \([25/77,30/77]\) and \([43/130,61/130]\), respectively.
Under the previous conditions, if \(q\) divides \(2N\Lambda\) when \(q\) is odd or if \(q\) divides \(4N\Lambda\) when \(q\) is even, the plateaux correspond to forbidden zones (they carry zero probability) that are clipped at the extremes of the interval \([0,1/2]\).
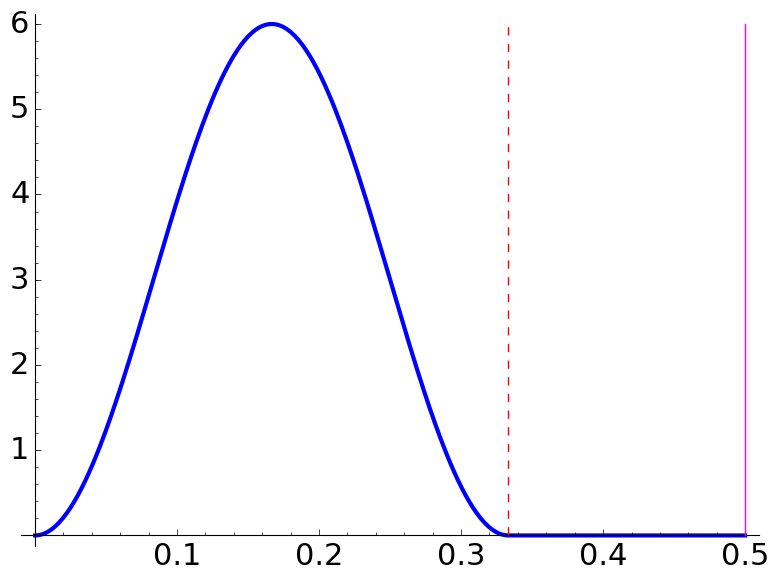
|
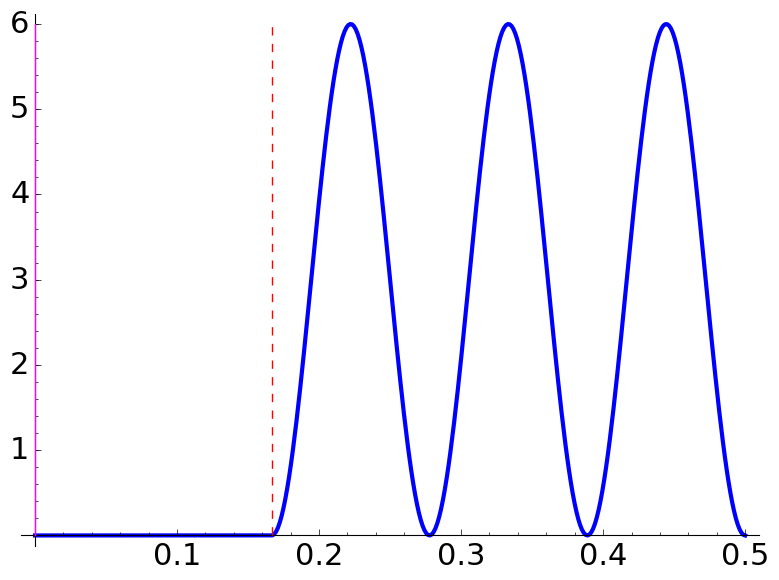
|
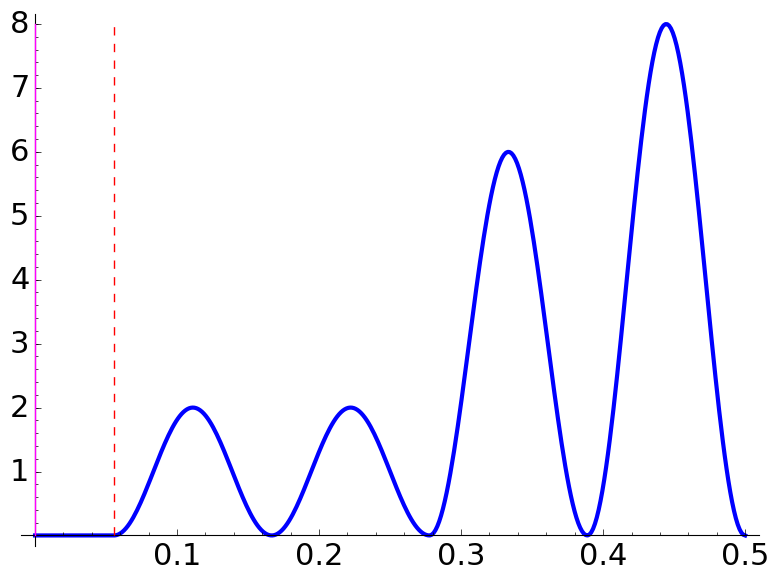 |
| \(\Lambda=\dfrac32,\) \(\dfrac aq=\dfrac{5}{3},\) \(N=1\) | \(\Lambda=\dfrac32,\) \(\dfrac aq=\dfrac{1}{6},\) \(N=3\) | \(\Lambda=\dfrac32,\) \(\dfrac aq=\dfrac{7}{18},\) \(N=3\) |
Using the formulas, the forbidden zones are \([1/3,1/2]\), \([0,1/6]\) and \([0,1/18]\), respectively. The rule is that for \(q\) odd they appear in the right extreme and for \(q\) even in the left extreme.
The proofs of the results mentioned here and a more detailed study of the expanded infinite well are the contents of a forthcoming joint paper.
|