Have you seen
the classic and wonderful puzzle "The vanishing Leprechaun" by Pat
Patterson popularized in a Martin Gardner's books? With the code in
this page you will be able of creating your own simple version and
perhaps you can use it to grab your students' attention when teaching
congruences.
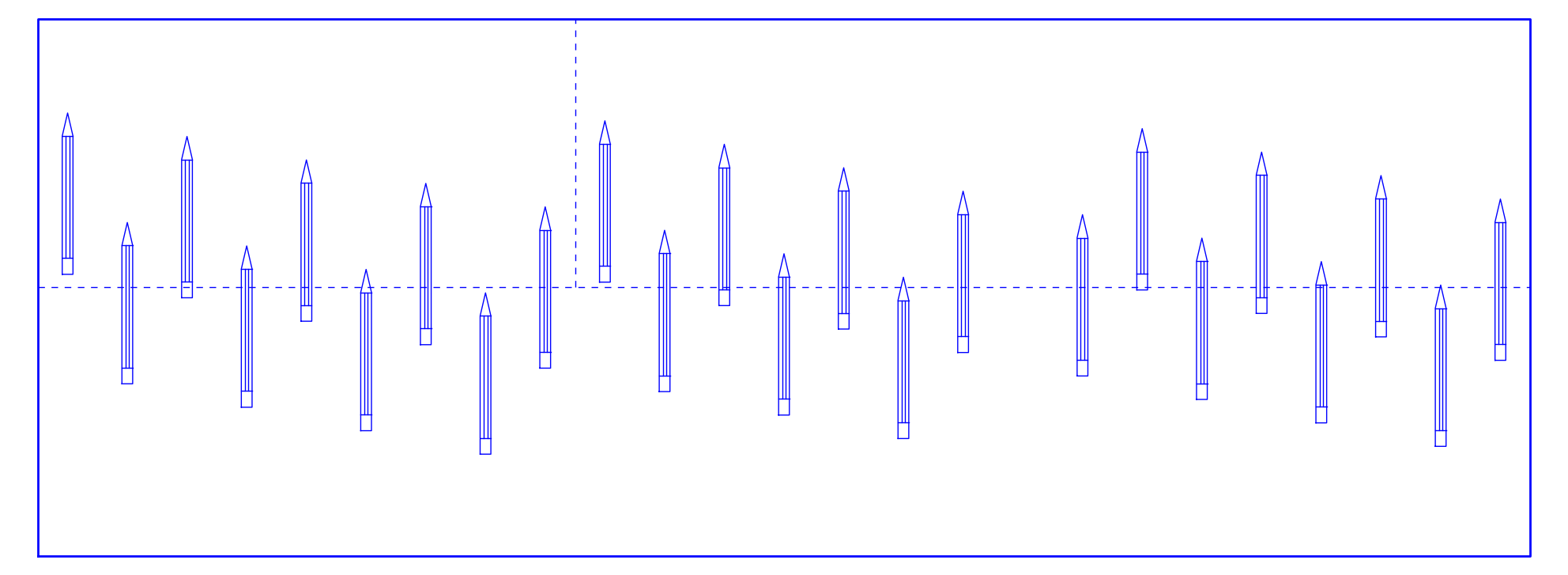
Here it is the output image with the default values:
Print the image (fullsize), cut
along the dashed lines and exchange the upper parts. Behold the magic,
24 pencils become 25! (of course, this "!" does not indicate a
factorial).
Where is the trick? Think about it for a moment. Perhaps a variant with single straight lines gives more insight.
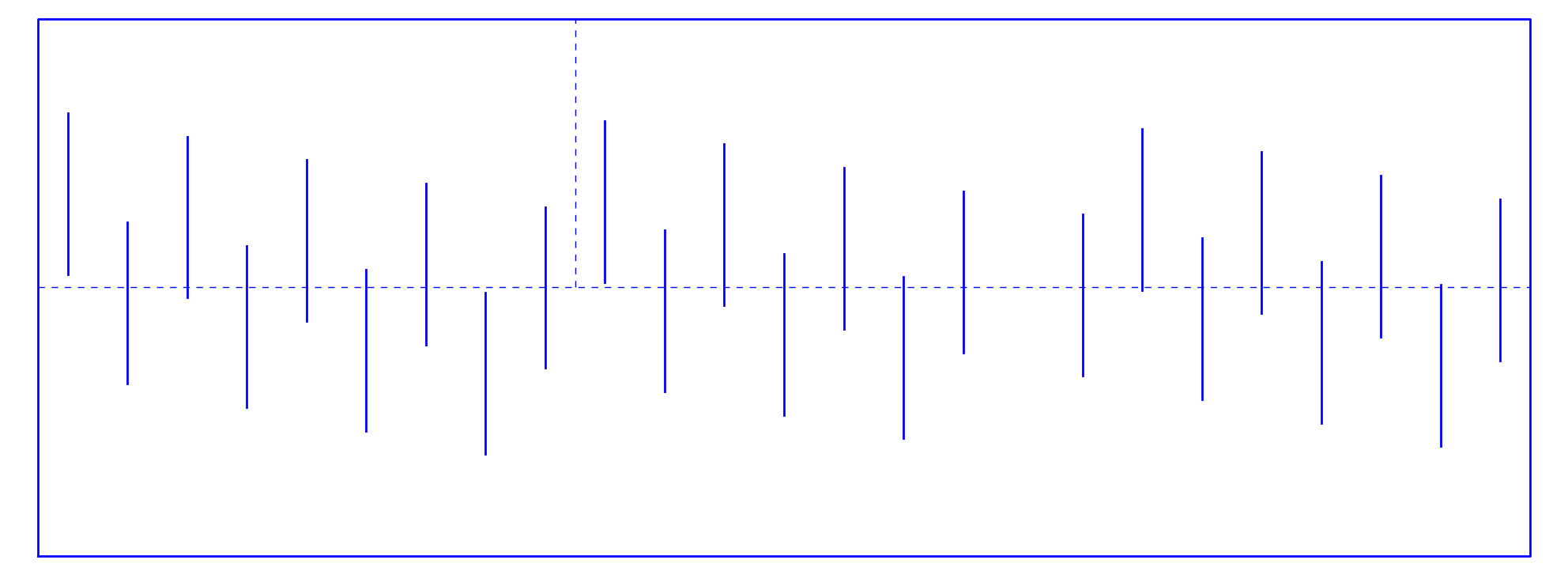 |
Still thinking? This is a big hint:
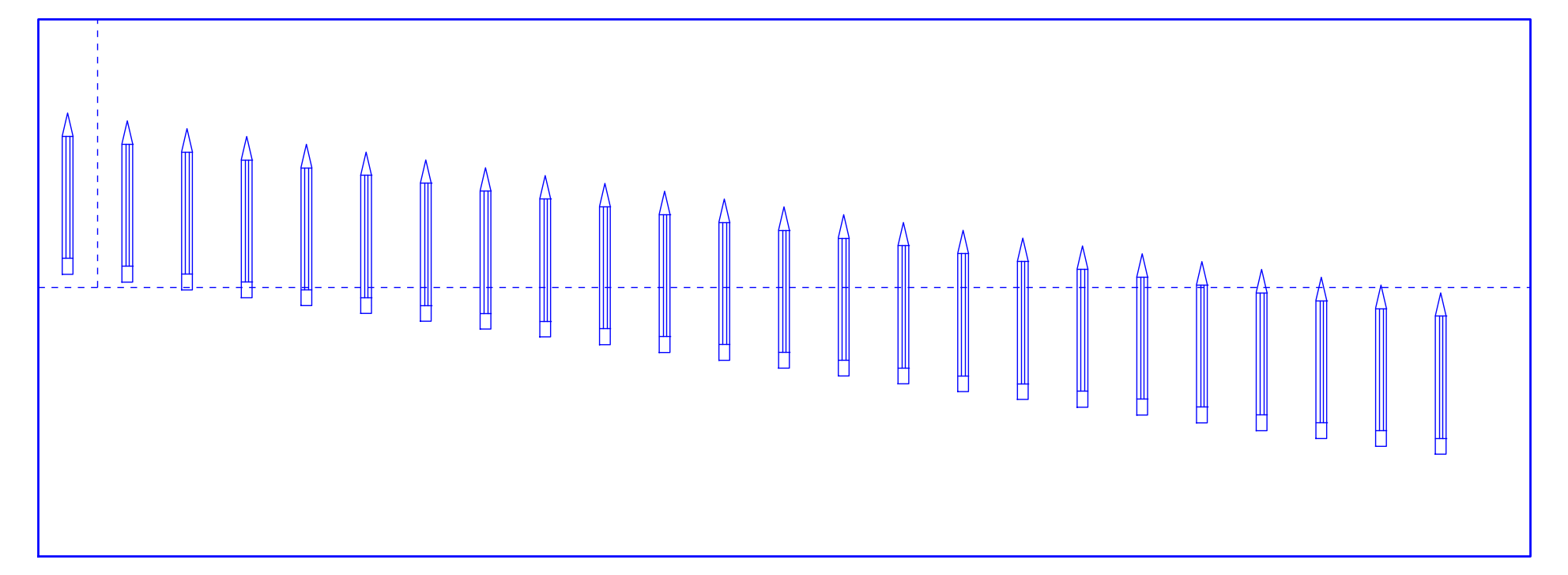 |
It is very easy to guess why in this image 24 becomes 25. In this
cyclic scheme, we are losing a little in the length of each pencil when
we move the right piece to the left. As there are many pencils we do
not note the difference and we have wood for a new pencil.
If you understand the trick in this case, the original one is the same,
simply we have used congruences modulo 25 to hash the position of the
24 pencils and the last empty space. The re-ordering is performed with
a linear function x->ax. Here a is related with D in the code below.
The sagemath code that produces the images above is:
def pencil(w,h,px,py):
px -= w/2
py -= h
# siloutte
L = [(0,0),(w,0),(w,6*h/7),(w/2,h),(0,6*h/7),(0,0)]
for k in range( len(L) ):
L[k] = (L[k][0]+px, L[k][1]+py)
P = line(L, thickness=1)
# vertical lines
L = [(0,h/10),(w/3,h/10),(w/3,6*h/7),(2*w/3,6*h/7),(2*w/3,h/10),(w,h/10)]
for k in range( len(L) ):
L[k] = (L[k][0]+px, L[k][1]+py)
P += line(L, thickness=1)
P += line( [(w/3+px,h/10+py),(2*w/3+px,h/10+py)], thickness=1)
P += line( [(px,6*h/7+py),(w/3+px,6*h/7+py)], thickness=1)
P += line( [(2*w/3+px,6*h/7+py),(w+px,6*h/7+py)], thickness=1)
return P
def mmissing(N,D,s,h,lin = 0):
hl = 0.3*h
# FRAME
P = line([(0,0),((N+1)*s,0),((N+1)*s,h),(0,h), (0,0)], thickness=2)
P += line([(0,h/2),((N+1)*s,h/2)], thickness=1, linestyle='--')
# MARK
P += line([(s*D,h/2),(s*D,h)], thickness=1, linestyle='--')
# PENCILS
for k in srange(N+1):
pno = (N*inverse_mod(N+1-D,N+1)*k)%(N+1)
offs = h - (1.7+pno)*0.05
sep = h/1.7/N
offs = (-hl-2*sep)/N*pno +hl+sep+h/2
if pno == N: continue
if lin == 0:
P += pencil( hl/10, hl, s/2+k*s,offs )
else:
P += line([(s/2+k*s,offs),(s/2+k*s,offs-hl)], thickness=2)
# P += text(str( pno ), (s/2+k*s,offs), fontsize=20)
return P
# N, N+1 is the number of pencils and D the "hash" value
# employed in the congruence.
# Choose N+1 and D coprime
N = 24
D = 1
# s and h are related to the size of the image
s = 0.4
h = 0.8*N/8
# Trivially ordered puzzle
P = mmissing(N,D,s,h)
P.set_aspect_ratio(1.5)
P.axes(False)
P.fontsize(20)
P.save('omissing2.eps', figsize = [20,20])
P.save('omissing2.png', figsize = [20,20])
D = 9
# Nontrivially ordered puzzle
P = mmissing(N,D,s,h)
P.set_aspect_ratio(1.5)
P.axes(False)
P.fontsize(20)
P.save('pmissing2.eps', figsize = [20,20])
P.save('pmissing2.png', figsize = [20,20])
# Lines instead of pencils
P = mmissing(N,D,s,h,1)
P.set_aspect_ratio(1.5)
P.axes(False)
P.fontsize(20)
P.save('missing2.eps', figsize = [20,20])
P.save('missing2.png', figsize = [20,20])