The Meyer wavelet


The Meyer wavelet, or rather an instance of Meyer wavelets, is an orthonormal wavelet with a simple formula corresponding to the following code (see this)
def meyerw():
f = 4*cos(pi*x)/(1-4*x^2)
f += 8*cos(4*pi*x)/(1-16*x^2)
f += 24*x*sin(2*pi*x)/(1-16*x^2)/(1-4*x^2)
F = f(x = 2/3*(x+1/2) )/3/pi
return F

Its graph is

mewp

It is remarkable to have an infinitely differentiable orthonormal wavelet in L1 with a fully explicit formula.

From this mother wavelet one construct an orthonormal basis of each subspace Wj of the multiresolution analysis (the orthogonal complement of Vj ). The aspect of the basis functions in the interval [-4,3] for small values of j is:

memhgen3m
 memhgen2m memhgen1m
j = -3
 j = -2
 j = -1


memhgen0
 memhgen1 memhgen2
j = 0
 j = 1
 j = 2


The previous graphs were plotted with the SAGE code:
def pl_gen(j,K):
f = meyerw()
P = point([(0,0)], size = 0)
for k in srange(-K,K+2):
ff = f( x= 2^j*x-k )*2^(j/2)
P += plot(ff, x, -4,3)
P.fontsize(15)
return P
 def pla_gen():
for j in srange(-3,3):
P = pl_gen(j, 50)
fname = './images/memhgen'+str(abs(j))
if j<0: fname += 'm'
P.save(fname+'.png', figsize = [4,4])

Let us illustrate that the wjk(x)= 2j/2 w(2j x-k) form a basis of L2 expanding the Mexican hat function
mexh



def pls_mh():
mh = (1-x^2)*exp(-x^2/2)/sqrt(2*pi)
P = plot(mh, -8,8, thickness= 3)
P.set_aspect_ratio(10)
P.fontsize(15)
P.save("./images/mexh.png")

The green line is the original function and the red line is there approximation using wjk with |j|<=J

memh0015
J = 0

memh0115
J = 1

memh0215
J = 2

memh0315
J = 3

memh0415
J = 4

For these plots the range of k was taken ridiculously large. Let us see the effect of reducing it to -K<=k<=K+1 with K = 1.
memh0015l
J = 0, K = 1

memh0115l
J = 1, K = 1

memh0215l
J = 2, K = 1

memh0315l
J = 3, K = 1

memh0415l
J = 4, K = 1

It is apparent that we are losing long distance information.


The code

This is the SAGE code for all the  images:

thi = 3

def meyerw():
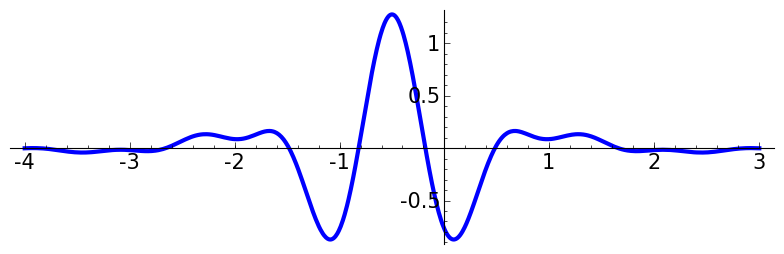
    f =  4*cos(pi*x)/(1-4*x^2)
    f += 8*cos(4*pi*x)/(1-16*x^2)
    f += 24*x*sin(2*pi*x)/(1-16*x^2)/(1-4*x^2)
    F = f(x = 2/3*(x+1/2) )/3/pi
    return F

def pls_mew():
    f = meyerw()
    P = plot(f, -4,3, thickness= thi)
    P.set_aspect_ratio(1)
    P.fontsize(15)
    P.save("./images/mewp.png")   

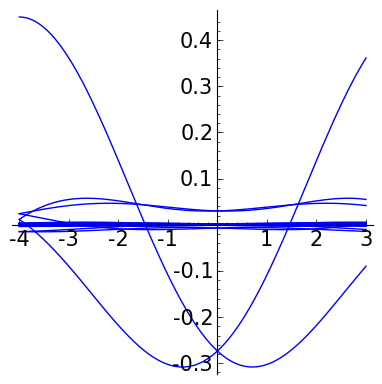
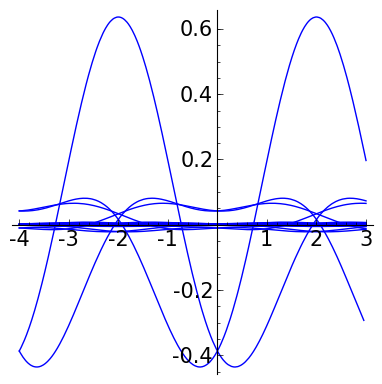
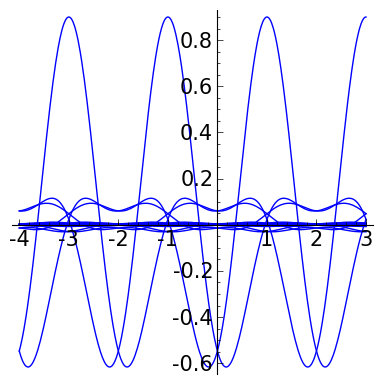
def pl_gen(j,K):
    f = meyerw()
    P = point([(0,0)], size = 0)
    for k in srange(-K,K+2):
        ff = f( x= 2^j*x-k )*2^(j/2)
        P += plot(ff, x, -4,3)
    P.fontsize(15)
    return P

def pla_gen():
    for j in srange(-3,3):
        P = pl_gen(j, 50)
        fname = './images/memhgen'+str(abs(j))
        if j<0: fname += 'm'
        P.save(fname+'.png', figsize = [4,4])


def pls_mh():
    mh = (1-x^2)*exp(-x^2/2)/sqrt(2*pi)
    P = plot(mh, -8,8, thickness=  3)
    P.set_aspect_ratio(10)
    P.fontsize(15)
    P.save("./images/mexh.png")   


def plo_bh2(F, a,b):
    h = (b-a)/350
    L = []
    ti = walltime()
    f =  4*cos(pi*x)/(1-4*x^2)
    f += 8*cos(4*pi*x)/(1-16*x^2)
    f += 24*x*sin(2*pi*x)/(1-16*x^2)/(1-4*x^2)

    for t in srange(a+1e-7, b+1e-7, h):
        S = 0.0
        for item in F:
            S += ( item[2]*2^(item[0]/2)*f(x = 2/3*(2^item[0]*t-item[1]+1/2) ) ).n()
        L.append( (t, (S/3/pi).n()) )
    P = list_plot(L, plotjoined= True, color='red')
    print '-----------'
    print 'plottime =', walltime(ti)
    print '-----------'
    return P


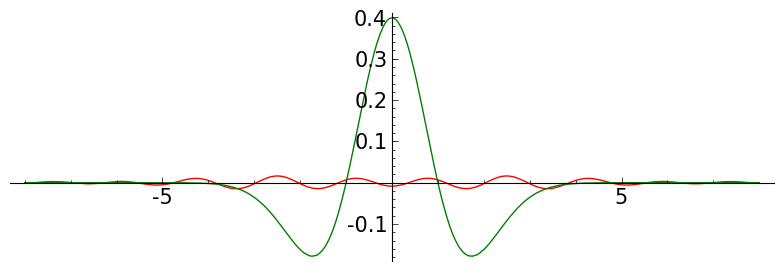
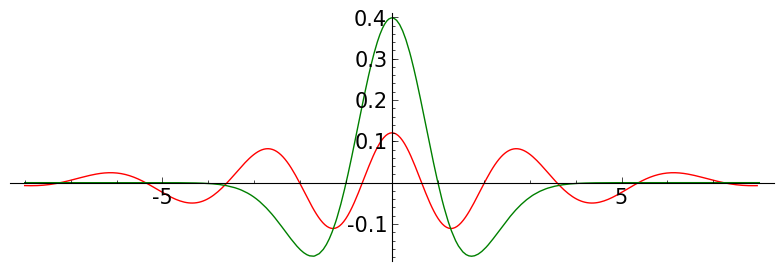
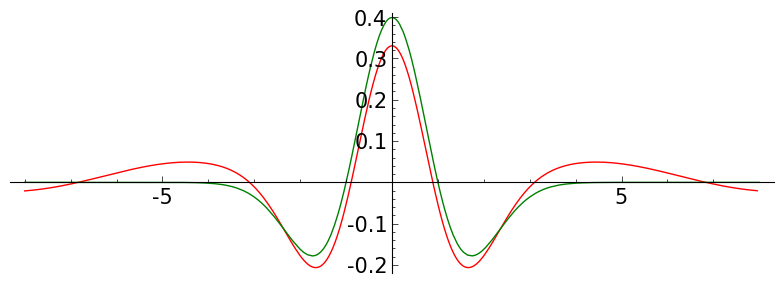
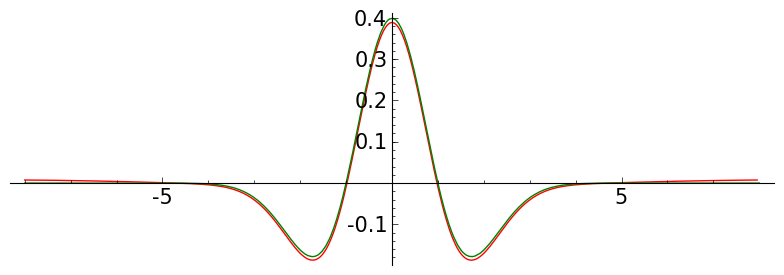
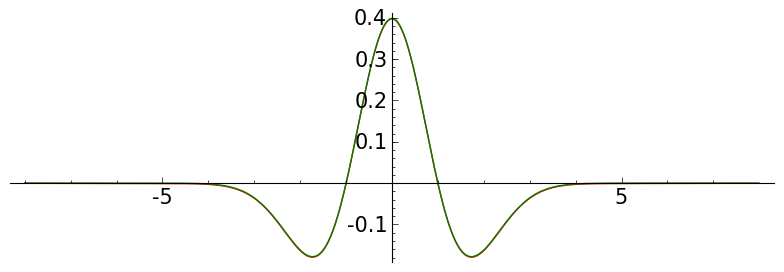
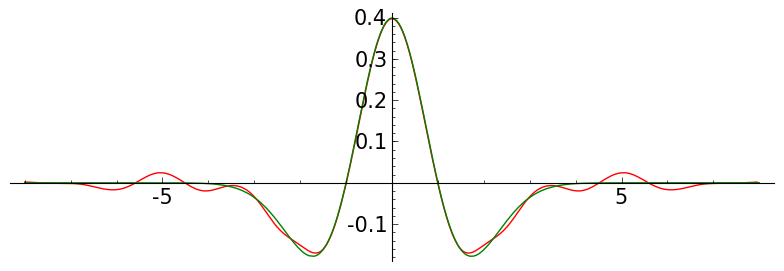
def meymh(J,K, a, b, ff):
    L = []
    ncoef = 0
    for j in srange(-J,J+1):
        for k in srange(-K,K+2):
            s = numerical_integral(meyerw()*2^(-j/2)*ff(x = (x+k)/2^j),  -oo,oo, max_points=500)
            r = s[0]
            if abs(s[0])>s[1]:
                L.append( (j,k,r) )
                print j,k,'->', r, s
                ncoef += 1

    print '-----------'
    print 'J =',J,'  K =',K, '  ncoef =',ncoef

    P = plo_bh2( L, a,b)
    P += plot(ff, x, a,b, color='green')

    P.set_aspect_ratio(9)
    P.fontsize(15)
    return P


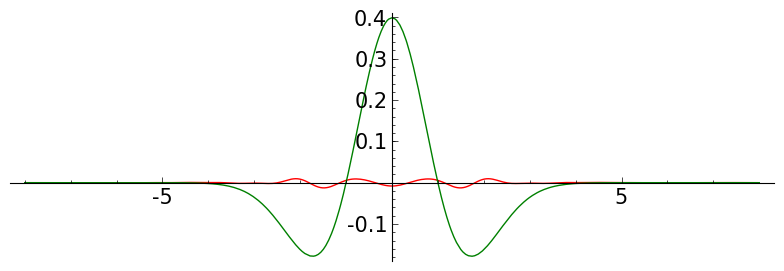
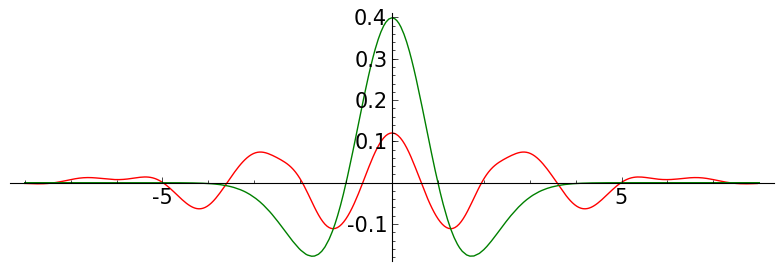
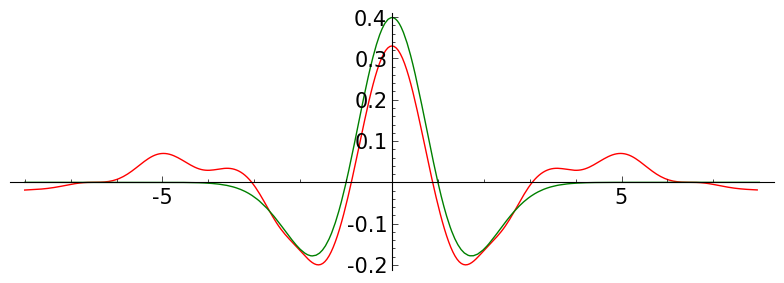
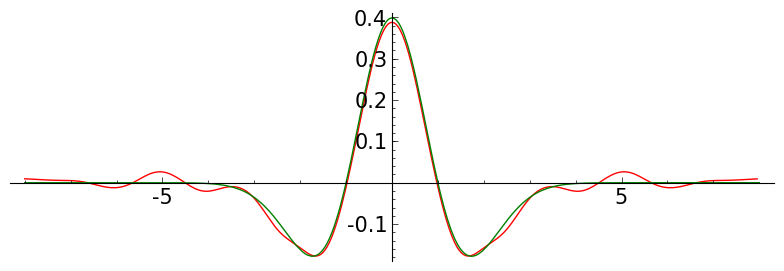
def to_four():
    ff = (1-x^2)*exp(-x^2/2)/sqrt(2*pi)
    for jj in srange(5):
        P = meymh( jj, 60 , -8,8, ff )
        P.save('./images/memh0'+str(jj)+'15.png')

def to_fourl():
    ff = (1-x^2)*exp(-x^2/2)/sqrt(2*pi)
    for jj in srange(5):
        P = meymh( jj, 1 , -8,8, ff )
        P.save('./images/memh0'+str(jj)+'l.png')

   
###################################################


pls_mew()
pla_gen()
pls_mh()
to_four()
to_fourl()