Splines are nearly local



The SAGE code below computes and plots the (natural) cubic spline interpolation with 2K+1 nodes in [0,1] when all the image values are 0 except the central one that is 1.

The results for K =4,5,6,7 are:

lspl4
9 nodes

lspl4
11 nodes

 
lspl4
13 nodes

lspl4
15 nodes

Click to enlarge the images.


The conclusion to be got from the quickly flat tails in these pictures is that cubic splines are almost local. If you perform cubic spline interpolation and you vary the image of a single node, it affects to the spline everywhere but you should not expect long distance noticeable effects.

It suggests the idea of using successfully B-splines (compactly supported splines) to get a cheap good approximation without interpolation.

The code

This is the SAGE code to produces the images:

def plot_spline(Y):
    # Make spline matrix
    N = len(Y)-1
    A = 4.0*identity_matrix(N+1)
    A += block_matrix([[ 0, identity_matrix(N) ], [ zero_matrix(1,1), 0 ]])
    A += block_matrix([[ 0, zero_matrix(1,1) ], [ identity_matrix(N), 0 ]])
    A[0,0] = 2
    A[N,N] = 2
    ############################
    #solve
    b = vector( Y[1:N+1]+[Y[N]] )
    b -= vector( [Y[0]]+Y[0:N] )
    d = A.solve_right(3*b)
    d = list(d)
    ############################
    # plot
    P = point([(0,Y[0])],size=0)
    P += list_plot(list((j/N,Y[j]) for j in srange(N+1)), size=100)
    for j in range(N):
        s1 = d[j+1]+d[j]-2*(Y[j+1]-Y[j])
        s2 = -d[j+1]-2*d[j]+3*(Y[j+1]-Y[j])
        P += plot( s1*(N*x-j)^3+s2*(N*x-j)^2+d[j]*(N*x-j)+Y[j], x, j/N,(j+1)/N, thickness=3)
    return P

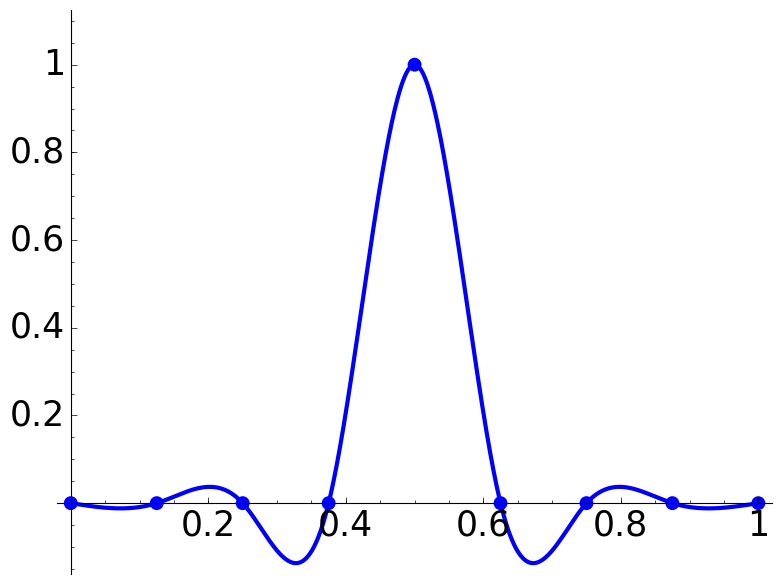
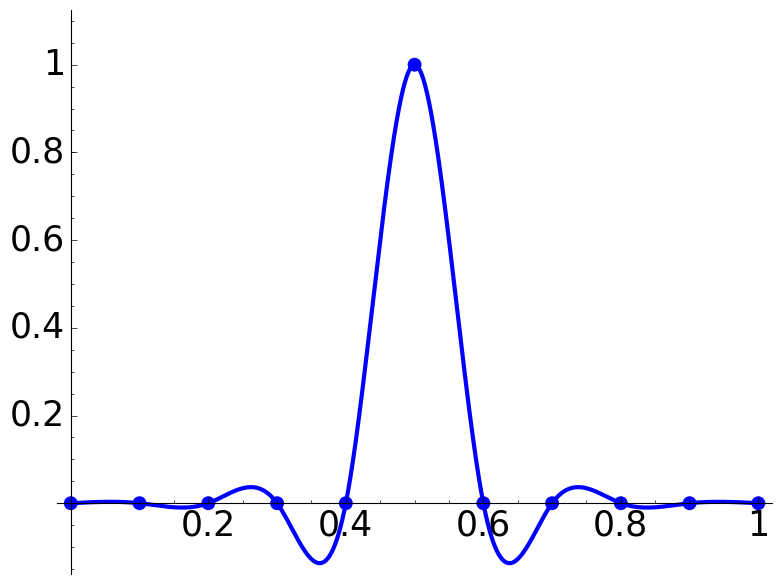
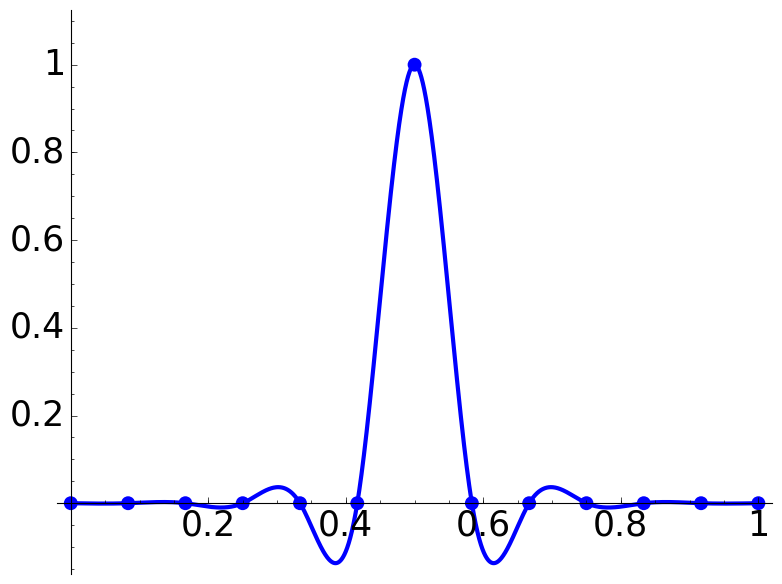
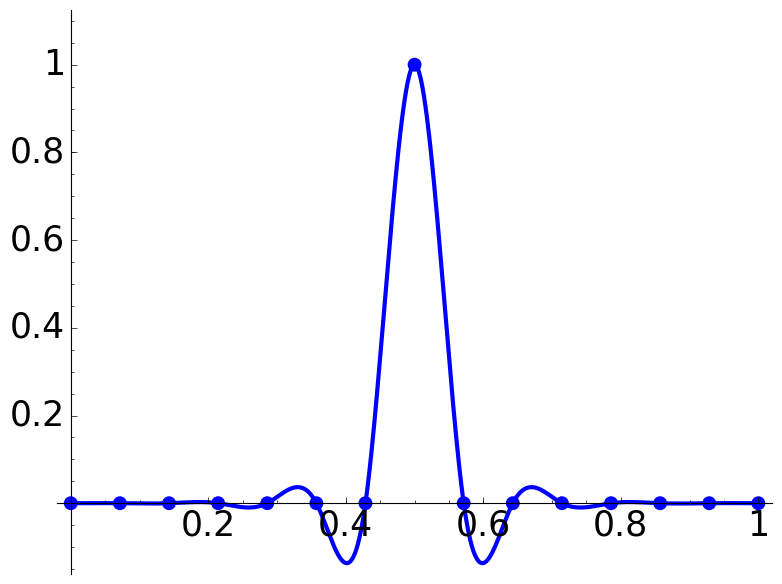
K = 7
he = 1.0
L = K*[0]+[he]+K*[0]
P = plot_spline(L) + point([(0,he*1.1)],size=0)
P.fontsize(25)
#P.set_aspect_ratio(1)
#P.axes(False)
P.show()