The Kuwahara filter

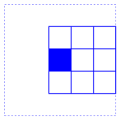
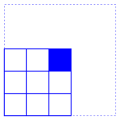
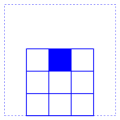
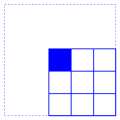
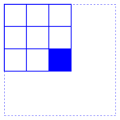
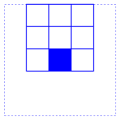
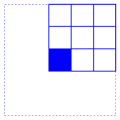
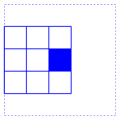
Sometimes one would like to have a selective blur not leaking the edges. This leads to difficult topological questions as a segmentation of the image into regions enclosed by not so well defined digitized curves. A cheap approach is the Kuwahara filter. Given a positive integer r, for each pixel we consider the squares of pixels of size 2r+1 containing it. For instance, for r=1 we have the 9 squares

The Kuwahara filter assigns to the selected filter the average tone of the square having the smallest variance of tones. In this way if an edge is the boundary of two more or less uniform zones, each pixel would be typically averaged with those in its zone.

A use of this filter is reducing the effect of the Gaussian noise or in general of any noise of zero average. A secondary use of this filter is to produce a water painting effect. The squares in the Kuwahara filter give a tile structure that recalls brushstrokes. To my taste, this is visually more appealing than the main use.

The octave code below implements the filter and applies it to produce several examples.

Let us start considering an image affected with a Gaussian noise of standard deviation 0.01. Here we have the original and the noisy image:

These are the results of applying the Kuwahara filter with different values of r:

The code

This is the octave code to produce the examples of the application of the Kuwahara filter:


pkg load image



clear all



name = '../images/sp2.png'



% original image

ima = imread( name );

ima = im2double(ima);



sig = 0.01



% noisy image (gaussian noise)

ima = imnoise(ima,'gaussian',0, sig);

imwrite(im2double(mat2gray(ima)),'./kuwn_0.png');



% kuwahara

for r = 3:5

  res = kuwa_f2( ima, r);

  imwrite(im2double(mat2gray(res)),sprintf('./kuwn_%d.png',r));

end





% water painting

name = '../images/bruch_r2_bw.jpg'

ima = imread( name );

ima = im2double(ima);



for r =2:4

  res = kuwa_f2( ima, r);

  imwrite(im2double(mat2gray(res)),sprintf('./kuww_%d.jpg',r));

end




function res = kuwa_f2( ima, r)



  d = 2*r+1;



  % standard deviation

  S = stdfilt(ima,ones(d),'symmetric');

%  S = stdfilt(ima,ones(d),'replicate');

%  S = stdfilt(ima,ones(d));



  % mean

%  M = imfilter(ima,ones(d)/d^2,'same', 'conv','circular');

%  M = imfilter(ima,ones(d)/d^2,'same', 'conv','symmetric');

%  M = imfilter(ima,ones(d)/d^2,'same', 'conv','replicate');

  M = imfilter(ima,ones(d)/d^2,'same', 'conv','replicate');





  %%%%%%%%%%%%%%%%%%%%%%%%%%%%



  tdim = size(S,1) * size(S,2);





  LS = zeros(0, tdim); % empty matrix

  LM = zeros(0, tdim); % empty matrix



  id = tic();

  for ki = -r:r

    disp([ki,round(toc(id))])

    fflush(stdout);

    for kj = -r:r

  %    circshift(S,[ki kj])

    

      LS = [LS; reshape( circshift(S,[ki kj]), [1,tdim] ) ];

      LM = [LM; reshape( circshift(M,[ki kj]), [1,tdim] ) ];

    end

  end





  [temp, mindexes] = min(LS,[],1);



  res = LM( sub2ind(size(LS), mindexes ,1:tdim) );



  res = reshape( res, [size(S,1), size(S,2)] );



endfunction


th = 3





def sgrid( po ):

  a, b = po[0], po[1]

  sq = point([po], size=0)

  for k in srange(4):

    sq += line([(a+k,b), (a+k,b+3)], thickness=th)

    sq += line([(a, b+k), (a+3,b+k)], thickness=th)

  return sq







for po in [(1,1), (0,2), (1,2), (2,2), (0,0), (1,0), (0,1), (2,0), (2,1)]:



  P = line( [ (0,0), (5,0), (5,5), (0,5), (0,0) ], thickness=1, linestyle='--' )

  P += polygon2d([ (2,2), (3,2), (3,3), (2,3) ])



  P += sgrid( po )





  P.fontsize(25)

  P.set_aspect_ratio(1)

  P.axes(False)

  name = '../images/kuw_sqxy.png'

  temp = name.replace('x',str(po[0])) 

  temp = temp.replace('y',str(po[1])) 

  print temp

  P.save(temp)

  #P.save('./borri.eps')


`r=3`		`r=4`		`r=5`