Julia & Newton


The matlab/octave code below applies the Newton-Raphson method in the complex plane to approximate the roots of the polynomial \(x^k-2\) for \(2\le k\le 5\) and distinguishes the attraction basins using different gray tones. In other words, the regions with the same gray tone correspond to the initial values \(x_0\) converging to the same root.

The Newton-Raphson algorithm for \(x^k-2\) is given by the recurrence formula \[x_{n+1}= \Big(1-\frac{1}{k}\Big) x_{n} +\frac{2}{kx_{n}^{k-1}}.\] The case \(k=2\) is somewhat special because the function defined by the right hand side applies the imaginary axis into itself (twice) and preserves the sign of the real part. If we assume that except for this axis the sequence converges, then we deduce at once that the basins of convergence are not very fancy, simply the left and right half planes. For \(k>2\) there is an involved fractal structure, as shown in the following figures.


june2 june3
\(k=2\) \(k=3\)

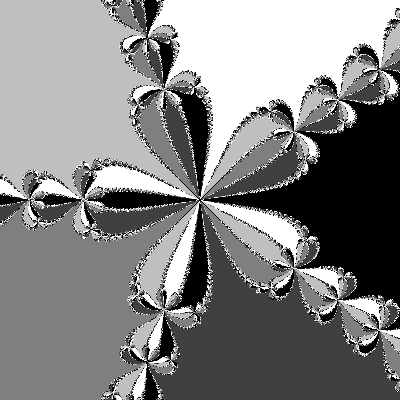
june4 june5
\(k=4\) \(k=5\)

The moral of the story is that deciding the convergence of the Newton-Raphson algorithm for a given starting value can be a hard problem even for simple functions.




The code

The images were created with matlab/octave. This is the octave version (for matlab, just omit the initial package loading).

pkg load image
pkg load signal

A = juliak(2, 20, 400, 0.01);
imwrite( A ,'june2.png' );

A = juliak(3, 30, 400, 0.01);
imwrite( A ,'june3.png' );

A = juliak(4, 180, 400, 0.1);
imwrite( A ,'june4.png' );

A = juliak(5, 380, 400, 0.1);
imwrite( A ,'june5.png' );
function R = juliak (k, Nmax, N, tol)
  % k = degree
  % Nmax = number of steps in Newton-Raphson
  % N = number of pixels
  % tol = tolerance
  
  A = meshgrid(linspace(-3/2,3/2,N),1:N);
  A = A + i*A' + eps;
  z = 2^(1/k)*exp(2*pi*i*[0:k-1]/k);
  
  % Newton-Raphson
  for l = 1:Nmax
    A = (1-1/k)*A+2/k*A.^(1-k);
  end

  R = zeros(N);
  for l = 1:k
    R = R + l*(abs(A-z(l))<tol);
  end
  
  % normalization
  R = im2double(mat2gray(R));
end
Main program
 Function juliak