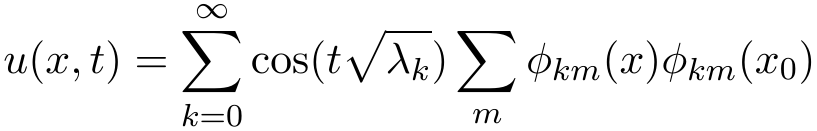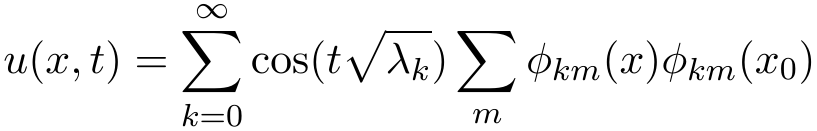The fundamental solution of the wave equation with initial zero
velocity in a compact Riemannian manifold is
where the lambda's are the increasingly ordered distinct eigenvalues
of the Laplace-Beltrami operator, the phi's are the corresponding
normalized eigenfunctions and x0
is the point of the manifold where the mass of the Dirac delta lies
at. The index m and the
(finite) summation on it regards the possibility of multiple
eigenvalues for the same eigenvalue (degeneracy).
In the case of the unit sphere with the usual Euclidean metric we
have exact and simple formulas for the eigenvalues and also exact
(but not so simple) expressions for the eigenfunctions, they are the
real spherical harmonics. This formula only makes sense when
considered as a distribution because at the initial time it is the
Dirac delta and the wave equation does not smooth data as opposed to
the heat equation.
If we truncate the series, then for t=0 we obtain a peak
approximating the Dirac delta. The wave equation gives an
approximation of how vibrations evolve, then we can considered the
truncated solution as an approximation of the evolution of a
pinch applied on a elastic sphere. Here we show the figures of the
numerical results. The scale of the pinch in terms of the radius has
been adjusted to get a better visual effect. For details,
check the matlab code at the end of this page.
If you pinch a rubber sphere the first reaction is a quick and
severe rebound:

|

|

|

|
t = 0.0000
|
t = 0.1257 |
t = 0.2513 |
t = 0.3770 |
In the last image a "lump" shows up but with lesser strength
because part of the energy escapes with the huge wavefront
surrounding it.
This an other wavefronts travel towards the south pole
producing "love handles" on the sphere.

|

|

|

|
t = 0.6283
|
t = 1.0053 |
t = 1.3823 |
t = 1.7593 |
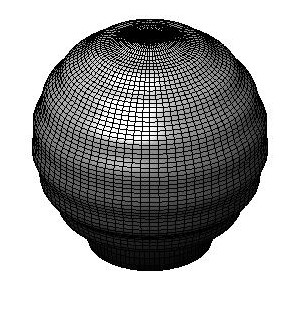
The waves interfere in the south pole to give a negative pinch that
rebounds. Note that the pinch and the rebound occurs at a time close
to pi, reflecting the fact that waves travel with speed one.

|
|

|

|
t = 2.2619
|
t = 2.6389 |
t = 3.0159 |
t = 3.3929 |
As expected, the waves come back to the north pole giving a north
pinch.
After the works of Colin
de Verdière, Chazarain
and Duistermaat
and Guillemin, we know that in general the trace has a
singular support contained in the integer multiples of the length of
the geodesics. This sounds natural in our case, because due to the
symmetry the trace should be as sitting on the north pole and
measuring the amplitude there for each time (analytically, one can
appeal to the spherical
harmonic addition theorem and the normalization Pl(1)=1). The rationale is that we have to wait
2*pi, the length of a meridian, to notice the same peak because the
waves travel with speed one. On the other hand, the trace for
the truncated series is a simple exponential sum and the
frequencies (the square roots of the eigenvalues) are close to k+1/2
for large values of k. Hence one should observe negative
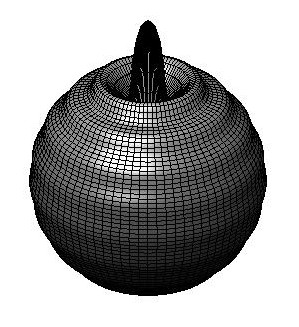
peaks at odd multiples of 2*pi. This can be difficult to observe in
the previous figures because the rebound is very quick. Let us see
the last instants before t=2*pi with a small step:
|

|

|

|
t = 6.0947
|
t = 6.1575 |
t = 6.2204 |
t = 6.2832 |
Although analytically is clear, I do not see a geometric reason for
this change in the phase when the time is increased by 2*pi,
specially when one compares the situation with the 1D case
corresponding to the unit circle. Note also that by the same
analytic reason, at t=pi the peak should be negligible
at the south pole because cos(t(k+1/2)) becomes close to zero.
The code
The matlab code used to generate the images is:
[Note: I confess that I realized too late that the spherical
harmonic addition theorem,
or the symmetry if you prefer, allows to write a simpler and
much
faster program. I keep this code because I want to do also some
experiments with other particular solutions of the wave equation
under
other non-symmetric initial conditions].
nframes = 51
maxl = 20
scale = 0.85;
res = [80,80];
phi = linspace(0,2*pi,res(1));
theta = linspace(0, pi,res(2));
[phi,theta] = meshgrid(phi,theta);
for k = 0:nframes-1
t = 2*pi*k/(nframes-1)
S = ones(res)/sqrt(4*pi); % sum. The initial
value is Y00
for l=1:maxl
[k,l]
P = legendre(l,cos(theta));
for m=-l:l
%--compute Y_{lm}
Plm = squeeze(P(abs(m)+1,:,:));
base = sqrt(
((2*l+1)/(2*pi))*factorial(l-abs(m))/factorial(l+abs(m)) )*Plm;
if m>0
Ylm = base.*cos(m*phi);
elseif m == 0
Ylm = base/sqrt(2.0);
else
Ylm = base.*sin(-m*phi);
end
%-----
S = S + Ylm*Ylm(1,1)*cos(t*sqrt(l*(l+1)));
end
end
rho = 1 + scale*S*12.0/maxl/maxl;
%
https://es.mathworks.com/help/matlab/examples/animating-a-surface.html
r = rho.*sin(theta); % convert to Cartesian
coordinates
x = r.*cos(phi);
y = r.*sin(phi);
z = rho.*cos(theta);
figure(1)
s = surf(x,y,z);
colormap gray
camlight right; lighting gouraud
% camlight right; lighting phong
view([40,30])
camzoom(1.5)
axis ([-3 3 -3 3 -3 3])
axis off
namefig = './images/sph%d_%d.jpg';
namefig = sprintf(namefig,maxl,k);
saveas(gcf,namefig)
pause(1)
end
Some obvious variations apply to generate short time variation
around 0 and 2*pi.