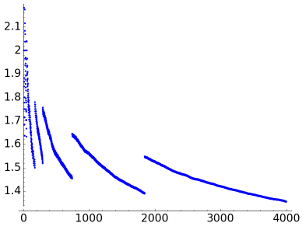
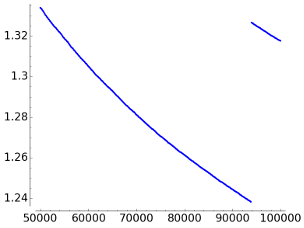
N in [10,4000) N in [50000, 100000) The compression algorithms LZ78 and LZW are dictionary methods having the property of universality. It means that they tend to reach the entropy bound, they are asymptotically optimal.
The functions
clz78
and
clzw
in the code below give the encoding with the corresponding algorithms of any text string not including the character #
that is employed as an EOF symbol.
The
clzw
function has an optional argument specifying the initial dictionary required by the LZW algorithm. If this argument is omitted then it is considered automatically the minimal dictionary containing all the characters in the text string input.
For instance, clz78( 'ban bananas!!!' ) gives
[(0, 'b'), (0, 'a'), (0, 'n'), (0, ' '), (1, 'a'), (3, 'a'), (6, 's'), (0, '!'), (8, '!')]
clzw( 'ban bananas!!!' )
[3, 2, 4, 0, 6, 4, 7, 2, 5, 1, 15]
[' ','!','a','b','c','n','s'] which adds the unneeded character 'c', the result is
[3, 2, 5, 0, 7, 5, 8, 2, 6, 1, 16]
Uncommenting print(L_dic) in these functions, the dictionary is displayed. In the previous example they are respectively
['', 'b', 'a', 'n', ' ', 'ba', 'na', 'nas', '!', '!!', '#']
[' ', '!', 'a', 'b', 'n', 's', 'ba', 'an', 'n ', ' b', 'ban', 'na', 'ana', 'as', 's!', '!!', '!!#']
Perhaps the name "dictionary method" is a little misleading because the dictionary is not a list of shorthand abbreviations to be included in the header of the compressed file (as in Huffman encoding). The dictionary is rather a subdivision of the file and only appears in the encoding-decoding process.
The implementations of the dictionary methods in practice may deviate from the theoretical model because they can include extra steps like a previous division of the file. The functions
ratio_lz78
and
ratio_lzw
compute the number of bits per character required by the pure encoding with LZ78 and LZW of a random generated string of length N composed by zeros and ones.
As they are universal methods, these ratios must tend to 1 because
a random list of N bits cannot be compressed (the entropy of a Bernoulli distribution p=1/2 is 1, if you prefer so).
The function plot_files
tests this and includes it in graphic files for
N in [10,4000) and also in [50000, 100000) with increments of 150. This function needs the data files built with make_datafile. It can take very long depending on your computer.
For LZ78 the graphs of the number of bits per character are
 |
 |
|
N in [10,4000) |
N in [50000, 100000) |
 |
 |
|
N in [10,4000) |
N in [50000, 100000) |
It is apparent that there is a strange band behavior. One may suspect that the function ceil explains it because it quantifies that the number of bits needs to represent nonnegative integers less than a certain number jumps each dyadic interval, but if we smooth ceil to the identity, the band structure persists. Another possible failed explanation is that outliers in the maximum can rule the output of this function during a while, but a representation of the successive maxima in the encoding reveals much shorter and random plateaus. Summing up, I have not a convincing explanation for this structure.
The conclusion after looking at these figures is that the convergence to 1 is very slow.
Repeating this experiment with gzip, an open source application for compression based on LZ77, for N=100000 I got 1.277, which is comparable to the result in our case. This ratio with gzip was still 1.272 for N=108.
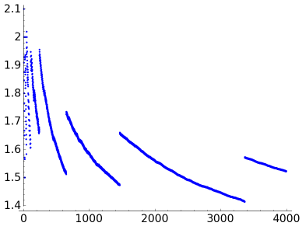
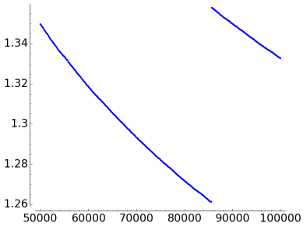
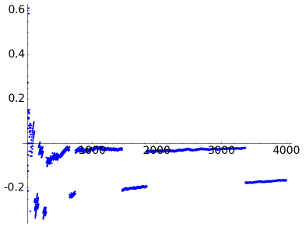
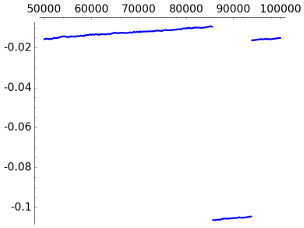
If we plot the difference between the number of bits per character for LZ78 and LZW, the result is
 |
 |
|
N in [10,4000) |
N in [50000, 100000) |
This implies that except for some small irrelevant values, in this example LZ78 is better. It is unclear to me if for "real life texts" typically LZ78 outperforms LZW or vice-versa. It is possible to find on the internet opinions in both directions.
This is the SAGE code that produces all the images:
|