A curious product

A consequence of the modular properties of the Dedekind \(\eta\) function and of the evaluation of \(|\eta(i)|^2\) is that for any positive divisor \(a\) of \(B^2+1\), \(B\in\mathbb{Z}\), we have the astonishing formula \[\sqrt{\frac{\pi}{a}} e^{-\pi/(6a)} \prod_{n=1}^\infty 2 e^{-2\pi n/a} \Big( \cosh \frac{2\pi n}{a} - \cos \frac{2\pi n B}{a} \Big) = \bigg( \int_{-\infty}^\infty e^{-\pi^4t^4}\, dt \bigg)^2.\] The right hand side is the constant \(0.3329679355\dots\)

The curious point is that there is some arithmetic here. If the divisibility condition does not hold, then the identity is not true in general. For related information see this outreach paper

For each \(a\), we have a set \(\mathcal{C}(a)\) of solutions of \(B^2\equiv -1\pmod{a}\). It is well known that for \(a\) prime \(\mathcal{C}(a)\) is empty if \(a\equiv -1\pmod{4}\), it has cardinality \(2\) if \(a\equiv 1\pmod{4}\) and, obviously, \(\mathcal{C}(2)=\{1\}\). The number of cardinality in the composite case can be decided essentially using the Chinese remainder theorem. The following figures, plotted with sagemath code below, explore for some small values of \(a\) to what extent there are real values \(B\not\in\mathcal{C}(a)\), \(B\in [0,a]\), such that the identity is true. Namely, the figures are the graph of the left hand side minus the constant of the right side when \(a\) is fixed and \(B\) varies in \([0,a]\).

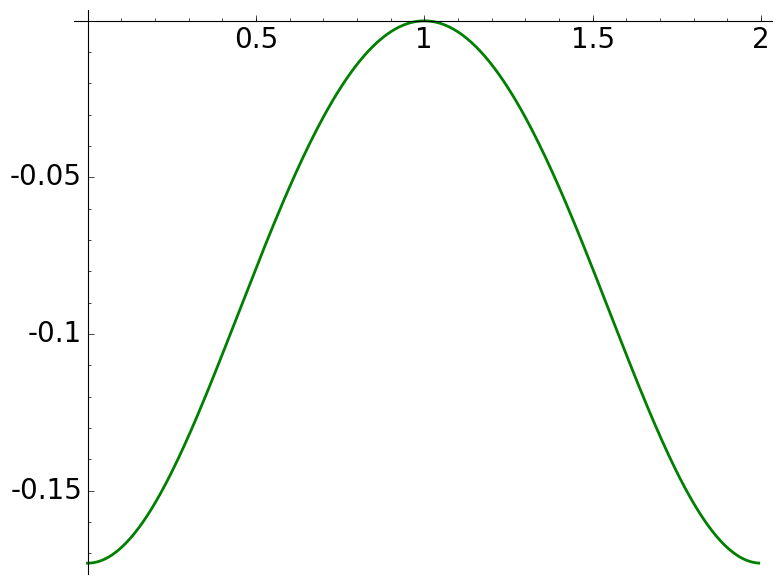
For \(a=2\), we have \(2\mid 1^2+1\) and the following figure shows that actually \(B=1\) is the only zero and the function is nonpositive.

\(a=2\), \(\mathcal{C}(a)=\{1\}\)

For \(a=5\), we have \(5\mid 2^2+1, 3^2+1\). Again, \(B=2,3\) are the only zeros. they are double zeros and the function is nonpositive.

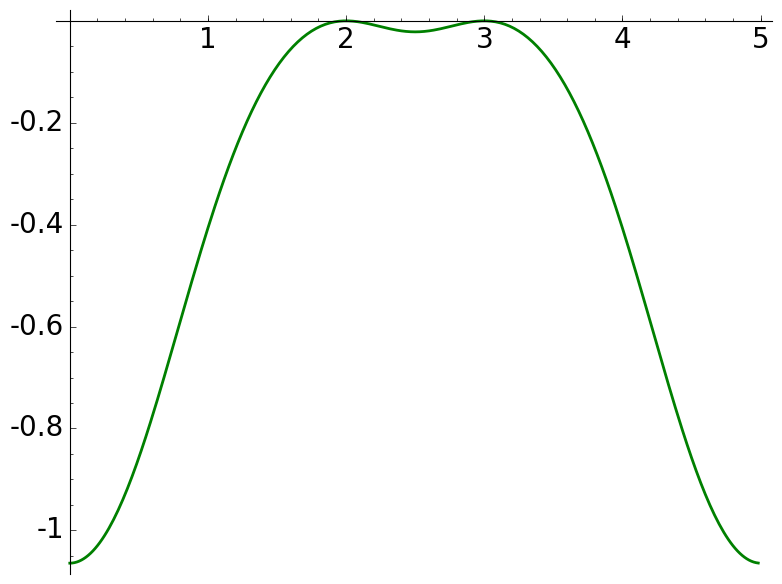\(a=5\), \(\mathcal{C}(a)=\{2,3\}\)

It is plain that \(3\nmid B^2+1\) for every \(B\in\mathbb{Z}\) but the graph reveals two symmetric real (non integral) zeros.

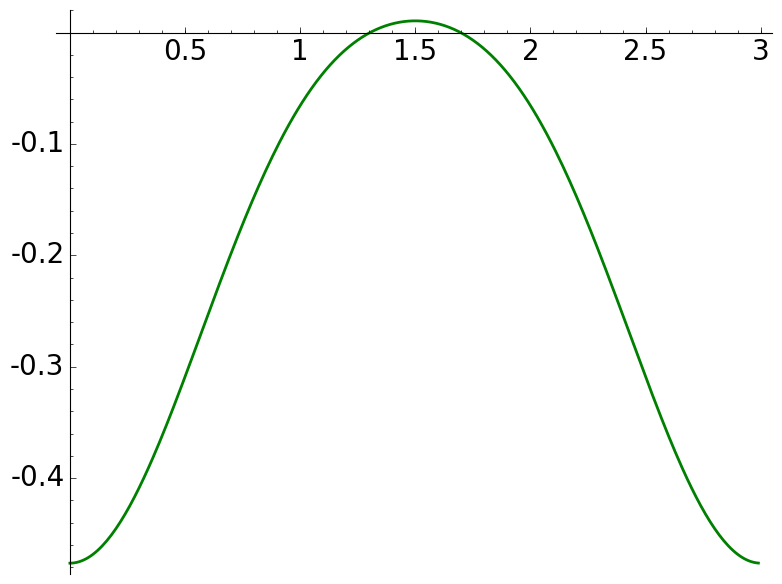\(a=3\), \(\mathcal{C}(a)=\emptyset\)

For \(a=10\), we have \(10\mid 3^2+1, 7^2+1\). Two zeros must appear at \(3\) and \(7\). The global graph does not allow to decide the number of extra real zeros to the naked eye.

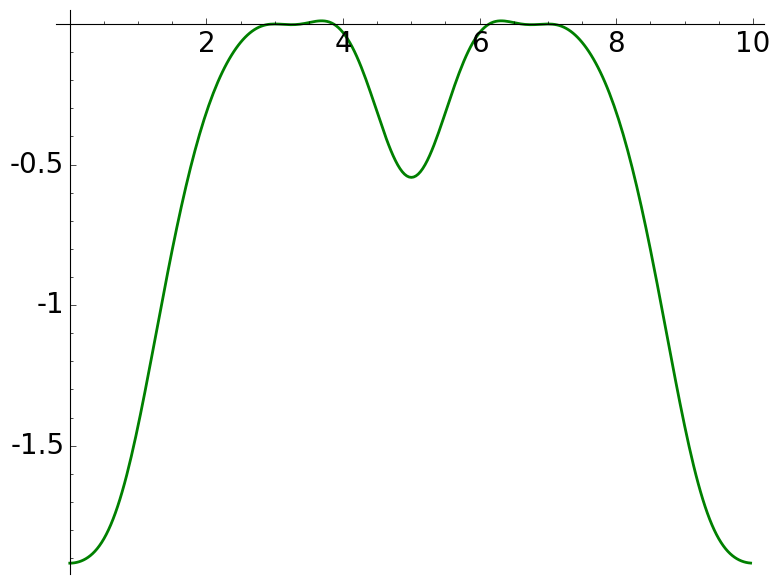\(a=10\), \(\mathcal{C}(a)=\{3,7\}\)

This is a zoom of the previous graph. By the symmetry, we deduce that there are four real zeros apart from For \(B=3,7\).

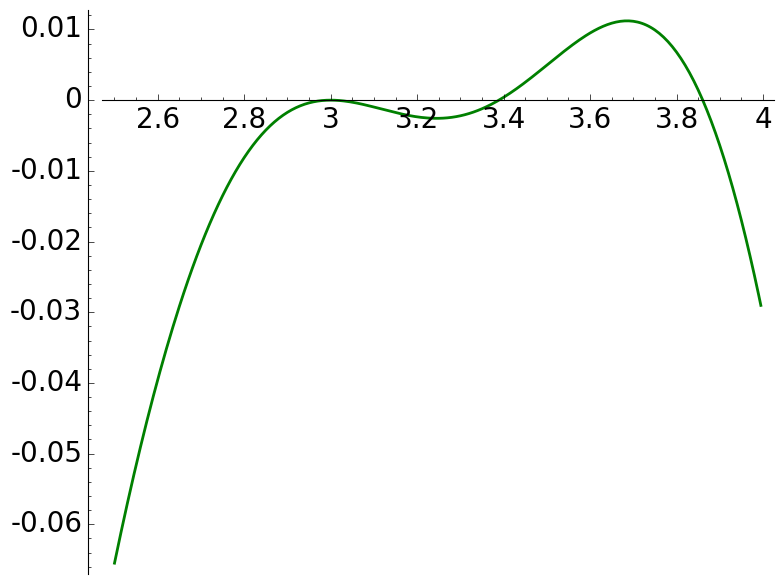\(a=10\), \(\mathcal{C}(a)=\{3,7\}\)

The code

This is the SAGE code that produces all the images:


N = 40



def ratp(b1,a1):

    # a_2=B_2=1

    Q = exp(pi/6-pi/6/a1)/sqrt(a1)

    P = 1

    for k in srange(1,N+1):

        P *= exp(2*pi*k*(1-1/a1))

        P *= cosh(2*pi*k/a1)-cos(2*pi*k*b1/a1)

        P /= cosh(2*pi*k)-1

        P = P.n()

    P = (P-1/Q).n()

    return P





def gra(a1,c,lb,ub):

    L = []

    h = (ub-lb)/300

    for b1 in srange(lb,ub,h):

        L.append((b1,ratp(b1,a1)))



    return list_plot(L,plotjoined=True,color= c, thickness=2, fontsize=20)



#P = gra(3, 'red',0,10)

#P += gra(10, 'green',0,10)

#P.set_axes_range(ymin=-0.02)



P = gra(2, 'green',0,2)

P.save('./images/cupr2.png')



P = gra(5, 'green',0,5)

P.save('./images/cupr5.png')



P = gra(3, 'green',0,3)

P.save('./images/cupr3.png')



P = gra(10, 'green',0,10)

P.save('./images/cupr10.png')



P = gra(10, 'green',2.5,4)

P.save('./images/cupr10d.png')