Avoidance of crossing


This is a curious phenomenon that I have learnt from the wonderful book Linear Algebra and Its Applications by P. Lax.
A generic curve in the space of symmetric matrices does not pass through matrices with multiple eigenvalues. In other words, if one plots the graphs determined by the eigenvalues along the curve, the graphs seem to avoid miraculously crossing each other. It seems that this phenomenon was firstly observed by physicists in the context of Quantum Mechanics.

The following graphs corresponding to the eigenvalues of A+tB with A and B random symmetric matrices (entries uniformly generated in [0,1]) and 0<t<1. They were created with the Matlab program included below.

1
 ncross1

A = [0.9912 0.2037 0.8272 0.6759; 0.2037 0.4758 0.3991 0.5994; 0.8272 0.3991 0.8214 0.8411; 0.6759 0.5994 0.8411 0.7008]

B = [0.7425 0.7579 0.3891 0.4293; 0.7579 0.5730 0.8497 0.2763; 0.3891 0.8497 0.9635 0.0859; 0.4293 0.2763 0.0859 0.9047]
2
 ncross2

A = [0.4519 0.3334 0.0591 0.7409; 0.3334 0.1999 0.4272 0.1687; 0.0591 0.4272 0.9418 0.0172; 0.7409 0.1687 0.0172 0.6505]

B = [0.7266 0.0945 0.8776 0.0144; 0.0945 0.1799 0.9263 0.0682; 0.8776 0.9263 0.6513 0.8646; 0.0144 0.0682 0.8646 0.6944]

3
 ncross3

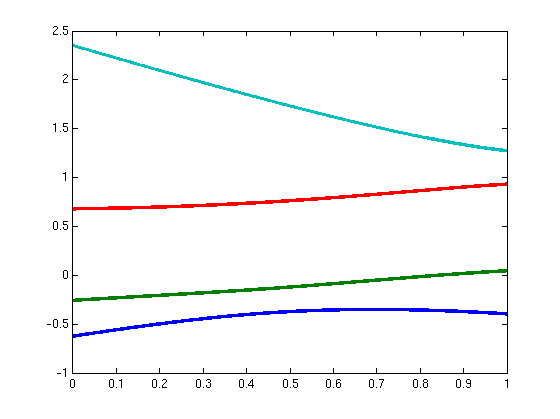A = [0.9158 0.1355 0.3321 0.8975; 0.1355 0.6153 0.5831 0.6983; 0.3321 0.5831 0.0321 0.8271; 0.8975 0.6983 0.8271 0.5815]

B = [0.9377 0.0478 0.0540 0.0206; 0.0478 0.5986 0.1140 0.7962; 0.0540 0.1140 0.0693 0.1360; 0.0206 0.7962 0.1360 0.2436]


4
 ncross4

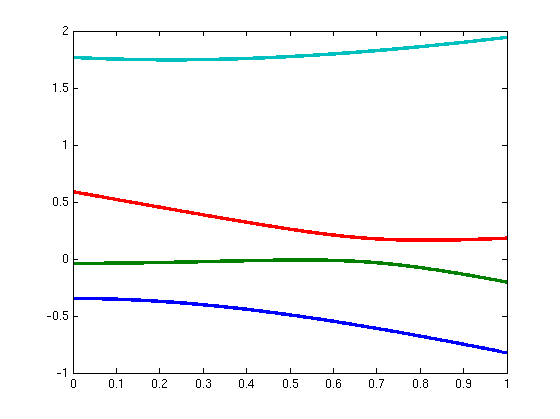A = [0.0686 0.2994 0.5916 0.2033; 0.2994 0.7984 0.5017 0.6508; 0.5916 0.5017 0.6008 0.1125; 0.2033 0.6508 0.1125 0.4982]

B = [0.2776 0.6525 0.9173 0.5098; 0.6525 0.1973 0.1112 0.2974; 0.9173 0.1112 0.3115 0.6938; 0.5098 0.2974 0.6938 0.3065]

5
 ncross5

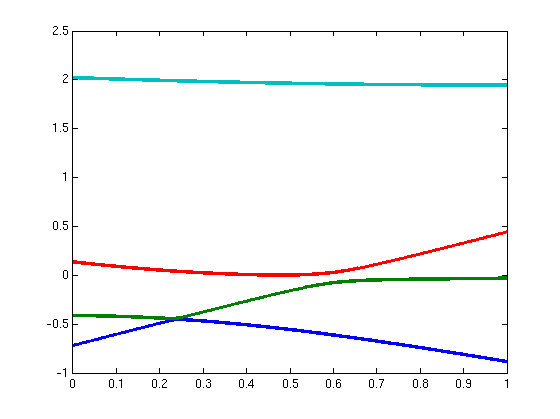A = [0.1056 0.5938 0.2827 0.1552; 0.5938 0.2836 0.5508 0.8709; 0.2827 0.5508 0.1310 0.8337; 0.1552 0.8709 0.8337 0.5047]

B = [0.4050 0.1736 0.5752 0.6062; 0.1736 0.5199 0.9892 0.4899; 0.5752 0.9892 0.0348 0.2928; 0.6062 0.4899 0.2928 0.5111]

6
 ncross1

A = [0.3668 0.7395 0.5247 0.8045; 0.7395 0.1895 0.1237 0.8210; 0.5247 0.1237 0.8960 0.5154; 0.8045 0.8210 0.5154 0.8553]

B = [0.3829 0.0846 0.7339 0.3320; 0.0846 0.3717 0.8282 0.1765; 0.7339 0.8282 0.0441 0.6867; 0.3320 0.1765 0.6867 0.9797]



Apparently two curves in 1 and 5 have crossings but after a zoom we observe:

1ncross1z
5ncross5z


The explanation is simpler than it seems. In a manifold of dimension N, two generic submanifold of dimensions a and b do not intersect if a+b<N. In this case the manifold is the space of nxn symmetric matrices then N = n(n+1)/2 (easy). The curve has dimension a=1 and the matrices with repeated eigevalues form a space of dimension b=N-2 (parametrize the matrices in terms of the eigenvalues and of an orthogonal basis of eigenvectors, think in the case n=2).


The code

Matlab program for the plots
 Program for the zoom
% dimension
N = 4;
% random matrices
A = rand(N,N);
B = rand(N,N);
%force symmetry
A = A+A';
B = B+B';
% number of points in plot
P = 400;
% with the standard output this gives almost 1pixel precision
R = zeros(N,P);
P = P-1;
for n=0:P;
    R(:,n+1) = eig((1-n/P)*A+n/P*B);
end
t = [0:1/P:1];
% plot graphs.
figure(1)
plot(t,R,'-','linewidth',3)
% ii = number of the low graph, [a,b] =interval
function zoomm( A,B, N, ii, a, b )
    % number of points in plot
    P = 400;
    % with the standard output this gives almost 1pixel precision
    R = zeros(N,P);
    P = P-1;
    for n=0:P;
        t = a + n*(b-a)/P;
        R(:,n+1) = eig((1-t)*A+t*B);
    end
    t = linspace(a,b,P+1);
    figure(2)
    plot(t,R(ii,:),'-', t,R(ii+1,:),'-','linewidth',3)