Anti-compression

Running this shell script that calls to this python code it is created a temp file of \(N\) random printable characters and compressed successively 15 times with gzip. The original size in bytes is \(N\). The size of the compressed file is shown on the console revealing a linear growth with the number of iterations.

Golden rule: Not every file can be compressed.

As a matter of fact, I employed this as part of the argument of the second chapter of my book.


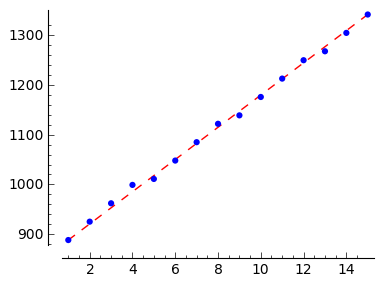
anti_comp3 anti_comp4
\(N=10^3\) \(N=10^4\)


anti_comp5 anti_comp6
\(N=10^5\) \(N=10^6\)


anti_comp7 anti_comp8
\(N=10^7\) \(N=10^8\)

Note that the printable characters are 96 (from the ASCII code 32 to 127) then the entropy is \(\log_2 96= 6.58\) and the optimal situation is to compress to \(6.58N/8=0.82N\) bytes. Theoretically LZ77 based compressors tend to this limit for large files and the first iteration is not far from it.


The following sagemath code including the obtained values was employed to plot the results:

L10_3 = [ (1,888), (2,925), (3,962), (4,999), (5,1011), (6,1048), (7,1085), (8,1122), (9,1139), (10,1176), (11,1213), (12,1250), (13,1268), (14,1305), (15,1342), 0]

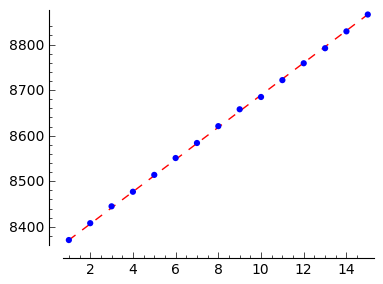
L10_4 = [ (1,8371), (2,8408), (3,8445), (4,8477), (5,8514), (6,8551), (7,8584), (8,8621), (9,8658), (10,8685), (11,8722), (12,8759), (13,8792), (14,8829), (15,8866), 0]

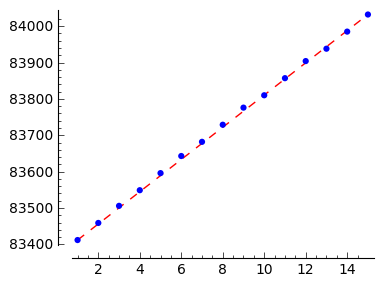
L10_5 = [ (1,83412), (2,83459), (3,83506), (4,83549), (5,83596), (6,83643), (7,83682), (8,83729), (9,83776), (10,83810), (11,83857), (12,83904), (13,83938), (14,83985), (15,84032), 0]

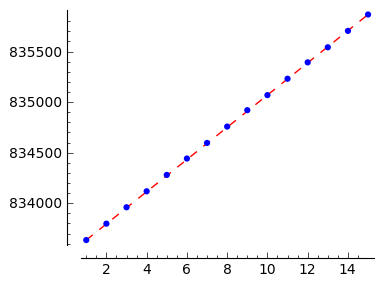
L10_6 = [ (1,833636), (2,833798), (3,833960), (4,834118), (5,834280), (6,834442), (7,834596), (8,834758), (9,834920), (10,835069), (11,835231), (12,835393), (13,835542), (14,835704), (15,835866), 0]

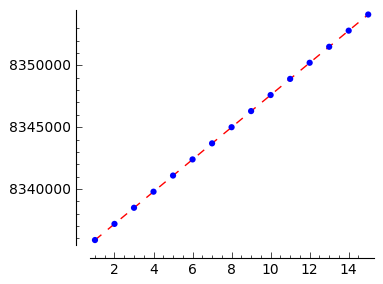
L10_7 = [ (1,8335856), (2,8337163), (3,8338470), (4,8339773), (5,8341080), (6,8342387), (7,8343688), (8,8344995), (9,8346302), (10,8347602), (11,8348909), (12,8350216), (13,8351510), (14,8352817), (15,8354124), 0]


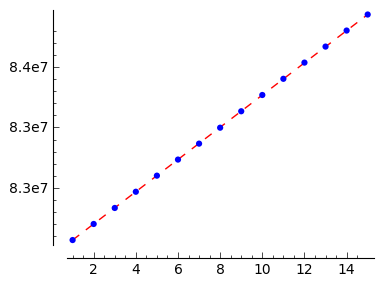
L10_8 = [ (1,83356883), (2,83370176), (3,83383420), (4,83396838), (5,83410152), (6,83423460), (7,83436644), (8,83449833), (9,83463429), (10,83476878), (11,83490281), (12,83503684), (13,83516933), (14,83530202), (15,83543469), 0]


L = L10_8[:]
P = list_plot(L[:-1], size=20, zorder=50)
P += line( [L[0], L[-2]], color='red', linestyle='--')
P.save( './anti_comp8.png', figsize=4)

The shell script

#!/bin/bash


N="1000"
./rand_text.py $N
echo $N

printf '[ '
for i in {1..15}
do
  gzip -f temp_anti.txt
  printf "(%d," "$i"
  stat --printf="%s), " temp_anti.txt.gz
  mv temp_anti.txt.gz temp_anti.txt
done
printf '0]\n'

# clean temp_anti files
rm temp_anti.txt



The python code

This is the rand_text.py code called by the script:



#!/usr/bin/env python
# -*- coding: iso-8859-15 -*-


import string, sys
from random import seed
from random import randint
seed(1)


N = int(sys.argv[1])

text = ''

for k in range(N):
  # random printable characters
  text += chr( randint(32, 127) )

try:
  with open("temp_anti.txt",'w') as sali:
    sali.write(text)

except IOError:
  sys.exit('\nI cannot write temp_anti.txt')